
- Details
- Written by: admin
- Category: UNNS Research
Formalizing Truth, Stability, Viability, and Existence
For centuries, mathematics has treated existence as a purely logical notion: if a definition is precise, consistent, and unambiguous, the object “exists.” UNNS introduces a radically different view. Existence is not a logical property, but a dynamical and geometric one.
In the UNNS Substrate, structures exist only if they can survive the operator chain: Φ (Generativity), Ψ (Coherence), τ (Curvature Stability), and XII (Collapse). This transforms mathematical objects into candidate universes, each tested for stability, projectability, and recursive viability.
- Details
- Written by: admin
- Category: UNNS Research
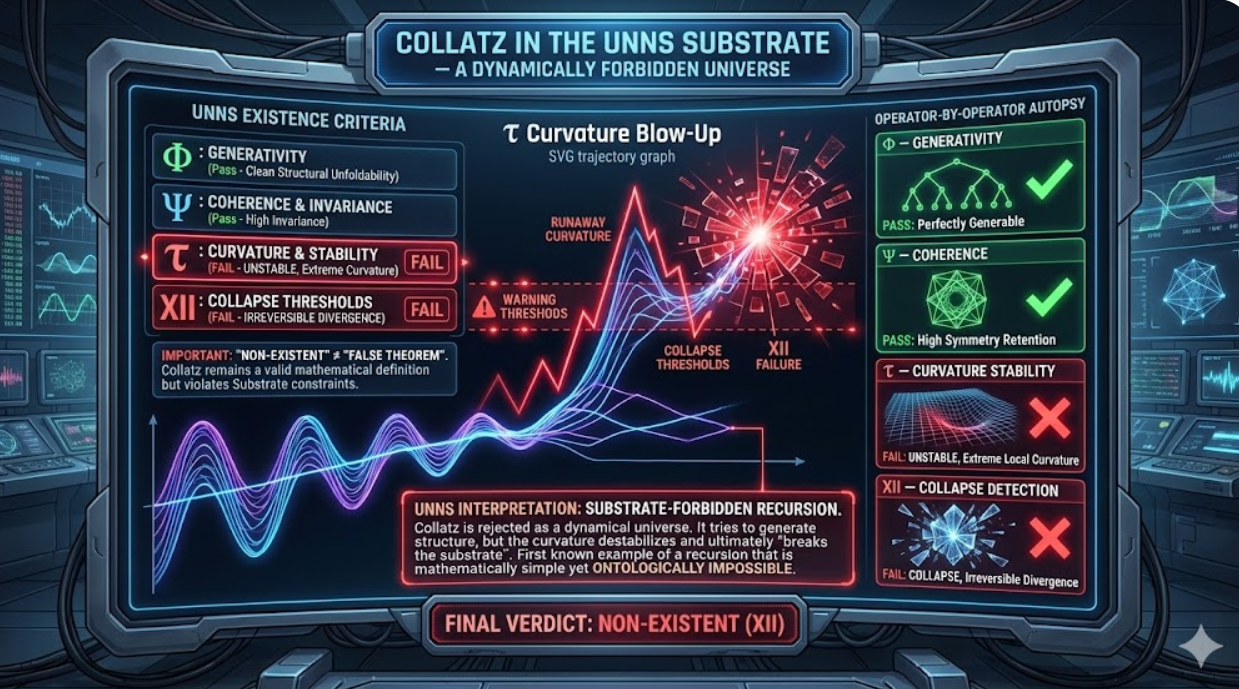
A Case Study in Dynamical Non-Existence within Recursive Worlds
Most mathematical structures pass quietly through Φ–Ψ–τ–XII analysis in Chamber XXVIII. Some become ADMISSIBLE. Some behave UNSTABLE (τ). A rare few strike the Substrate itself and are classified as NON-EXISTENT.
The Collatz recurrence belongs to this last category. In classical mathematics it is a simple algorithm. In UNNS, it becomes a recursion with catastrophic curvature: a structure that cannot exist inside a stable recursive universe.

- Details
- Written by: admin
- Category: UNNS Research
UNNS Substrate — Core Definition and Architecture
This document provides the official definition of the UNNS Substrate, its structure, its projection mechanics, and its foundational role within the UNNS framework. It supersedes all informal descriptions and should be treated as the canonical reference for researchers, developers, and contributors within the UNNS ecosystem.
- Details
- Written by: admin
- Category: UNNS Research
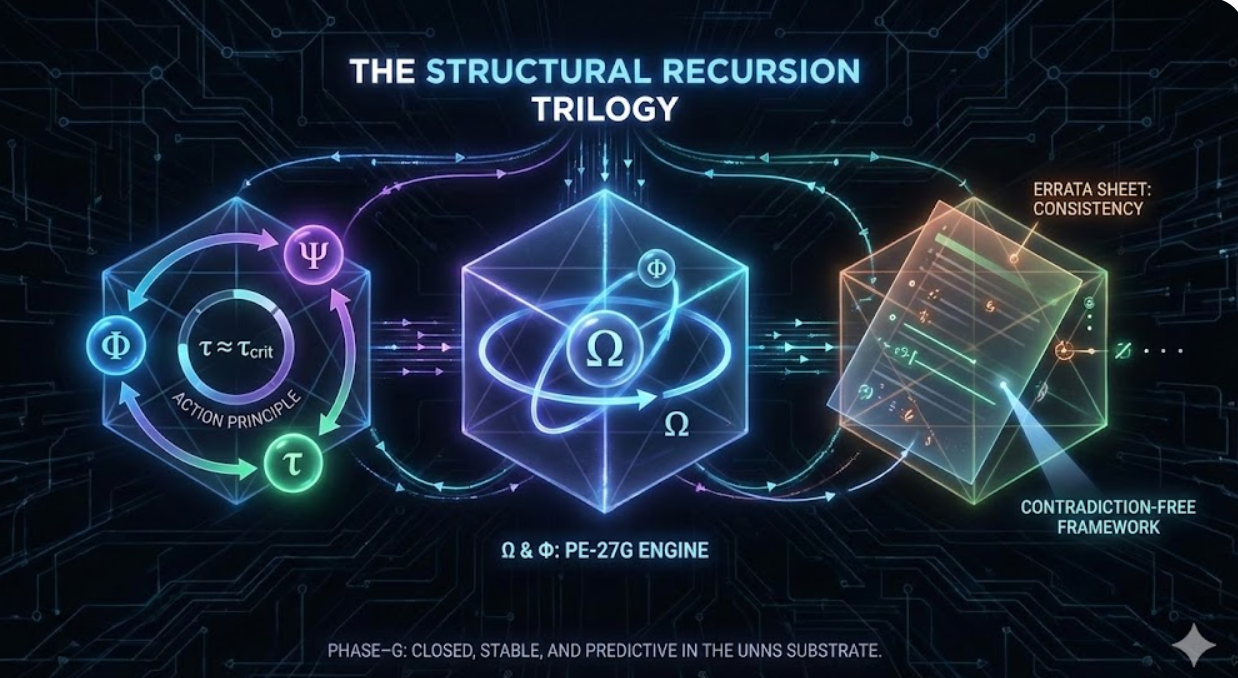
The Structural Recursion Trilogy
This article introduces three foundational UNNS Substrate papers that together define the Phase–G structural recursion framework: the closure operator Ω, the nonlinear manifold Φ, and the Φ–Ψ–τ action principle. They are presented here as a single trilogy that turns UNNS from an experimental lab engine into a coherent mathematical discipline.
- Details
- Written by: admin
- Category: UNNS Research
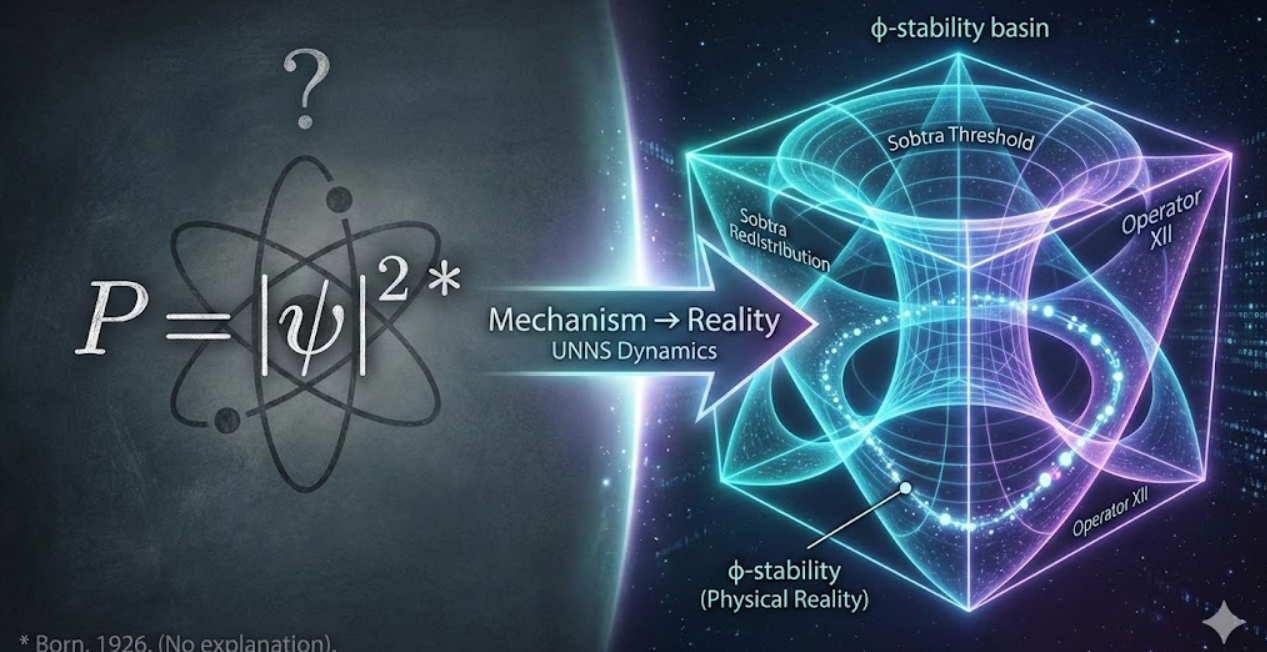
Mechanism → Reality
How UNNS Subsumes the Born Rule Through Sobra–Sobtra Dynamics
UNNS does not replace or contradict quantum mechanics. Instead, it reveals the geometric recursion that produces the Born rule and stabilizes quantum outcomes. The probabilistic interpretation remains empirically valid; UNNS simply supplies the underlying deterministic structure that makes it work.
Reference: Sobra–Sobtra Mechanism as the UNNS Replacement for the Born Rule (PDF)
In classical quantum mechanics, the Born rule appears suddenly and without explanation. Max Born added it in a footnote. Wolfgang Pauli extended it to the multi-particle case — also in a footnote.
In UNNS, this historical oddity becomes completely natural. Classical QM lacked Sobra thresholds, Sobtra redistribution, Operator XII collapse, and φ-recursion geometry — therefore the |ψ|² rule had to be “inserted” by hand.
UNNS does not assume probability. It generates φ-stability — a deterministic analogue of |ψ|² — through recursion, curvature, and threshold dynamics.
