A Case Study in Dynamical Non-Existence within Recursive Worlds
Most mathematical structures pass quietly through Φ–Ψ–τ–XII analysis in Chamber XXVIII. Some become ADMISSIBLE. Some behave UNSTABLE (τ). A rare few strike the Substrate itself and are classified as NON-EXISTENT.
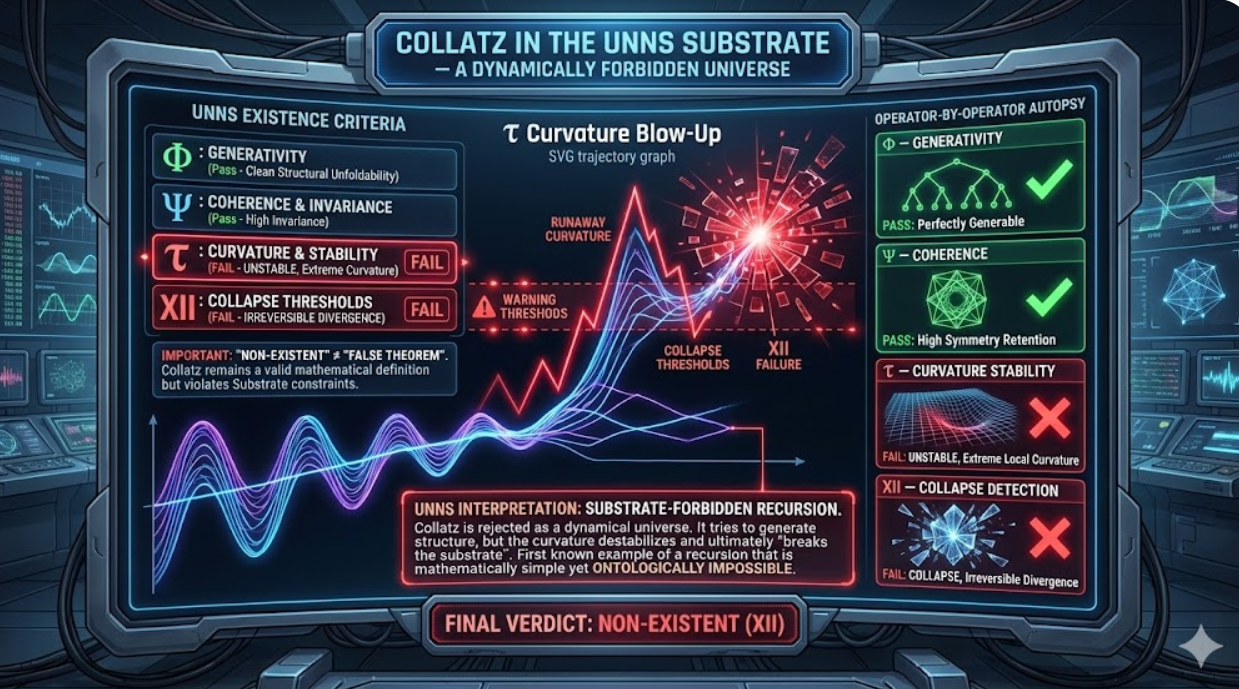
The Collatz recurrence belongs to this last category. In classical mathematics it is a simple algorithm. In UNNS, it becomes a recursion with catastrophic curvature: a structure that cannot exist inside a stable recursive universe.
1. What “NON-EXISTENT” Means in UNNS
UNNS treats existence as a dynamical property. A structure exists if and only if it can survive the operators:
- Φ: Generativity
- Ψ: Coherence and invariance
- τ: Curvature and stability
- XII: Collapse thresholds
“NON-EXISTENT” does not mean that the mathematics is false. It means the structure produces unbounded curvature or catastrophic projection failure — it cannot be embedded into the UNNS Substrate as a dynamical world.
The Collatz recurrence violates τ and XII constraints but remains a valid mathematical definition.
2. Why Collatz Fails: The τ–XII Trajectory
The Collatz recursion shows extreme local curvature spikes, followed by deep symmetry-breaking phases and an unbounded τ-trajectory. This causes XII to signal an irreversible divergence.
Inline Visualization — τ Curvature Blow-Up
This stylized SVG illustrates the characteristic pattern detected by the Chamber: oscillation → spike → collapse thresholds → runaway curvature → XII failure.
3. Operator-by-Operator Autopsy
Φ — Generativity
Collatz is perfectly generable. Φ confirms clean structural unfoldability.
Ψ — Coherence
The recurrence is syntactically and compositionally coherent. Ψ passes with high invariance and symmetry retention.
τ — Curvature Stability
This is the critical failure point: the structure develops extreme curvature and unbounded dynamical variation. τ marks Collatz as UNSTABLE.
XII — Collapse Detection
The τ-instability cascades into XII collapse. The Chamber reports an irreversible divergence inconsistent with substrate constraints.
4. UNNS Interpretation
Collatz is not rejected as a mathematical object. It is rejected as a dynamical universe.
- It tries to generate structure, but the curvature destabilizes.
- Its projection geometry cannot remain coherent.
- It ultimately “breaks the substrate.”
This is a new category introduced by UNNS: substrate-forbidden recursion.
Collatz becomes the first known example of a recursion that is mathematically simple yet ontologically impossible.
7. Collatz vs Banach Fixed Point — Two Universes Compared
To see what Chamber XXVIII is really measuring, it helps to compare Collatz with a structure that the Substrate loves. The Banach fixed-point example is almost the perfect opposite of Collatz: a quiet contraction map that gently folds trajectories towards a unique attractor.
Banach Fixed Point (Contraction Map)
x[n+1] = 0.5 * x[n] + 1
- Φ: Generable, linear, structurally simple.
- Ψ: High coherence and invariance; no branching or discontinuity.
- τ: Curvature decays; trajectories spiral inward to a fixed point.
- XII: No collapse; the structure is fully admitted.
- Verdict: ADMISSIBLE.
Collatz Recurrence (3n + 1)
x[n+1] = (x[n] % 2 == 0) ? x[n] / 2 : 3 * x[n] + 1
- Φ: Generable; the rule is clear and computable.
- Ψ: Structurally coherent, but piecewise and sharply branching.
- τ: Extreme curvature spikes; no stable attractor in the simulated domain.
- XII: Collapse triggered by irreversible divergence in τ-geometry.
- Verdict: NON-EXISTENT (dynamically forbidden by the Substrate).
Operator Comparison
| Operator | Banach Fixed Point | Collatz Recurrence |
|---|---|---|
| Φ — Generativity | Simple contraction, fully generable. | Piecewise rule, fully generable. |
| Ψ — Structural Consistency | Single smooth rule, strong invariance. | Branching structure; coherent but with rough transitions. |
| τ — Curvature Stability | Curvature decays; trajectories converge. | Curvature explodes; trajectories oscillate and spike. |
| XII — Collapse | No collapse; geometry stays well within substrate bounds. | Collapse detected; τ-trajectory violates substrate constraints. |
| UNNS Verdict | ADMISSIBLE — a fully realizable recursive universe. | NON-EXISTENT — a mathematically valid but dynamically forbidden universe. |
Trajectory Sketch
The contrast can also be pictured as two different kinds of τ-trajectories: one falling calmly into an attractor, the other oscillating into collapse.
In UNNS language, Banach describes a universe that folds into itself until a fixed structure emerges. Collatz describes a universe that keeps kicking the Substrate harder and harder, until τ-curvature and XII collapse declare it non-embeddable. The mathematics of both are valid; only one can exist as a stable recursive world.