Chamber XXVIII — Consistency Operator

Details
Written by: admin
Category: Labs

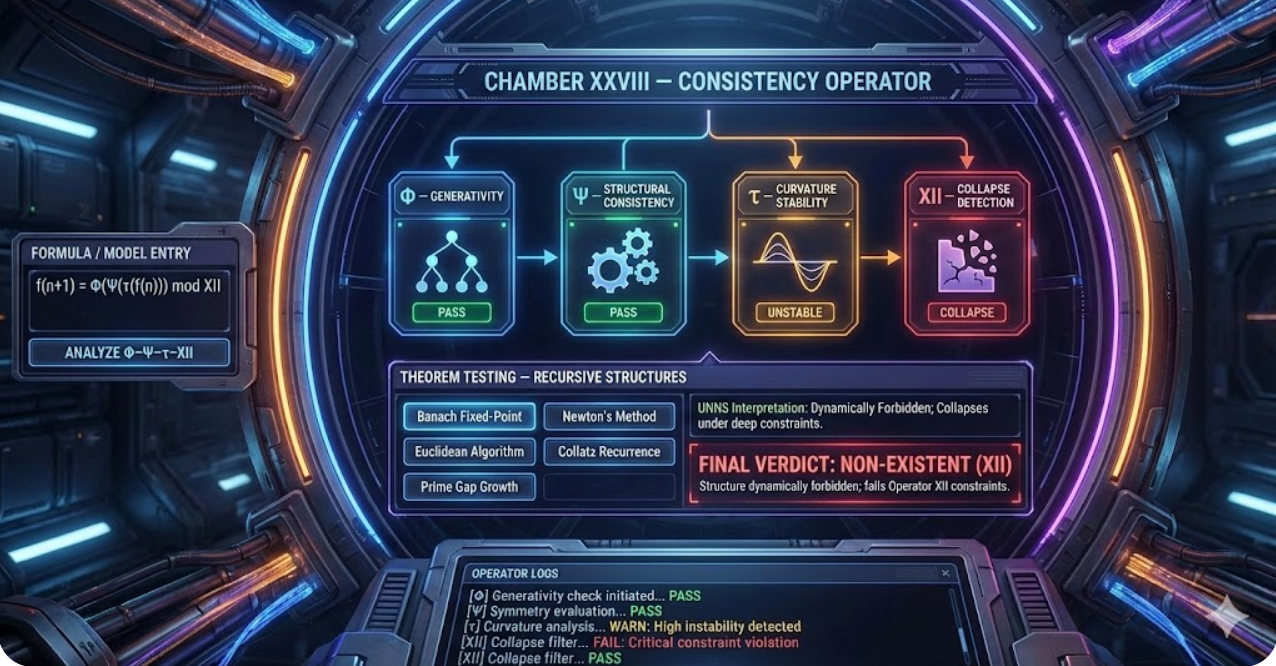
Φ–Ψ–τ–XII Structural + Recursive Dynamical Engine

Chamber XXVIII is the first UNNS laboratory built to answer a single question: “Can this structure exist in the UNNS Substrate?”

Unlike earlier Chambers, which focus on specific constants, fields, or τ-dynamics, Chamber XXVIII works one level higher. It accepts a formula, recursion, or simple model, and runs it through the full Φ–Ψ–τ–XII operator chain, treating the formula as a candidate universe inside the Substrate.

The result is not just a convergence test or a numerical diagnostic. It is an existence verdict in the UNNS sense: whether the structure is generable, coherent, τ-stable, and able to survive Operator XII collapse filters.

1. Interactive Chamber Embed

Use the embedded Chamber below to experiment directly with formulas, recursions, physical models, and theorem-inspired iterations.

Open Chamber XXVIII in fullscreen

2. The Four Operators: Φ, Ψ, τ, XII

Chamber XXVIII is driven by the Φ–Ψ–τ–XII recursion engine. Every input passes through four distinct stages:

  • Φ — Generativity: Can the structure be unfolded as a valid recursion?
  • Ψ — Structural Consistency: Are symmetry, coherence, and invariance preserved?
  • τ — Curvature Stability: Does the recursive trajectory remain geometrically stable?
  • XII — Collapse Detection: Does the structure survive deep substrate constraints?

Together, these stages act as a consistency engine: a way to test whether a candidate model can be hosted by the UNNS Substrate as a stable dynamical object.

Operator Flow Diagram

Φ Ψ τ XII

The Chamber interface mirrors this diagram: each operator has its own panel, numerical diagnostics, and a badge showing PASS, FAIL, STABLE, UNSTABLE, or COLLAPSE.

3. Theorem Testing and Real-World Models

One of the most powerful aspects of Chamber XXVIII is the Theorem Testing — Recursive Structures panel. Each button in this panel loads a carefully chosen recurrence inspired by a classical theorem or model:

  • Banach Fixed-Point Theorem: A stable contraction map.
  • Newton’s Method (sqrt(2)): Quadratic convergence under iteration.
  • Euclidean Algorithm (GCD): Recursive reduction via remainders.
  • Collatz Recurrence (3n + 1): A structurally simple but dynamically extreme map.
  • Prime Gap Growth Model: A heuristic recursion inspired by prime distributions.

When a theorem example is selected, the formula is loaded, analyzed automatically, and a short “UNNS Interpretation” line explains what the verdict means in substrate language. This makes Chamber XXVIII a bridge between classical mathematics and UNNS-style existence classification.

Theorem Testing Diagram

Theorem Recursion Φ–Ψ–τ–XII Engine Existence Verdict

In this way, each theorem is treated as a candidate “world” inside the UNNS Substrate. The Chamber does not decide whether a theorem is true or false, but whether its recursive formulation can exist as a stable dynamical object.

4. Reading the Verdicts

Chamber XXVIII outputs one of five possible top-level verdicts:

  • ADMISSIBLE: The structure passes all operators and can exist as a stable substrate object.
  • UNSTABLE (τ): Generable and coherent, but with dangerously high curvature.
  • INCOHERENT (Ψ): Fails structural invariance or projection consistency.
  • NON-GENERABLE (Φ): Cannot be unfolded as a valid recursion.
  • NON-EXISTENT (XII): Dynamically forbidden; the structure collapses under deep substrate constraints.

Existence Types Diagram

ADMISSIBLE UNSTABLE (τ) INCOHERENT (Ψ) NON-GENERABLE (Φ) NON-EXISTENT (XII)

The same language appears in the Chamber as badges next to each operator panel, and in the final verdict section. Over time, these five classes become a vocabulary for talking about “what kind of existence” a structure has in the UNNS Substrate.

5. How to Use Chamber XXVIII

Step 1 — Enter or Load a Formula

Type a recursion or model into the Formula / Model Entry box, or select a preset from the Load Example dropdown or the Theorem Testing buttons.

Step 2 — Run Φ–Ψ–τ–XII Analysis

Click Analyze. Φ tests generativity, Ψ checks structure, τ simulates the trajectory, and XII evaluates collapse conditions.

Step 3 — Read the Panels

Each panel offers numeric and qualitative feedback:

  • Φ shows generativity depth and recursion tree snapshots.
  • Ψ reports symmetry, coherence, and invariance scores.
  • τ plots curvature over time and reports stability metrics.
  • XII lists any triggered collapse conditions.

Step 4 — Interpret the Verdict

The final verdict block combines the operator results into a single existence classification. The operator logs at the bottom give a narrative of what happened, using Φ/Ψ/τ/XII labels and PASS/INFO/WARN/FAIL status tags.

6. The Role of Chamber XXVIII in the UNNS Project

Chamber XXVIII marks a turning point in the UNNS program: it turns the Substrate into a consistency engine for mathematics and physics.

Instead of asking only “Is this theorem true?” or “Does this model fit the data?”, we can now ask:

“Can this structure exist at all, as a dynamical object in the UNNS Substrate?”

The answer is not a proof, but a new kind of structural diagnosis. Some recursions are admitted. Some are unstable but allowed. A few are dynamically forbidden. The Chamber gives us a way to map that landscape and to see classical mathematics through the lens of recursive geometry and τ-curvature.

Chamber XXVIII is therefore both a tool and a statement: existence itself can be tested, operator by operator.

Main Menu