- Details
- Written by: admin
- Category: UNNS Research
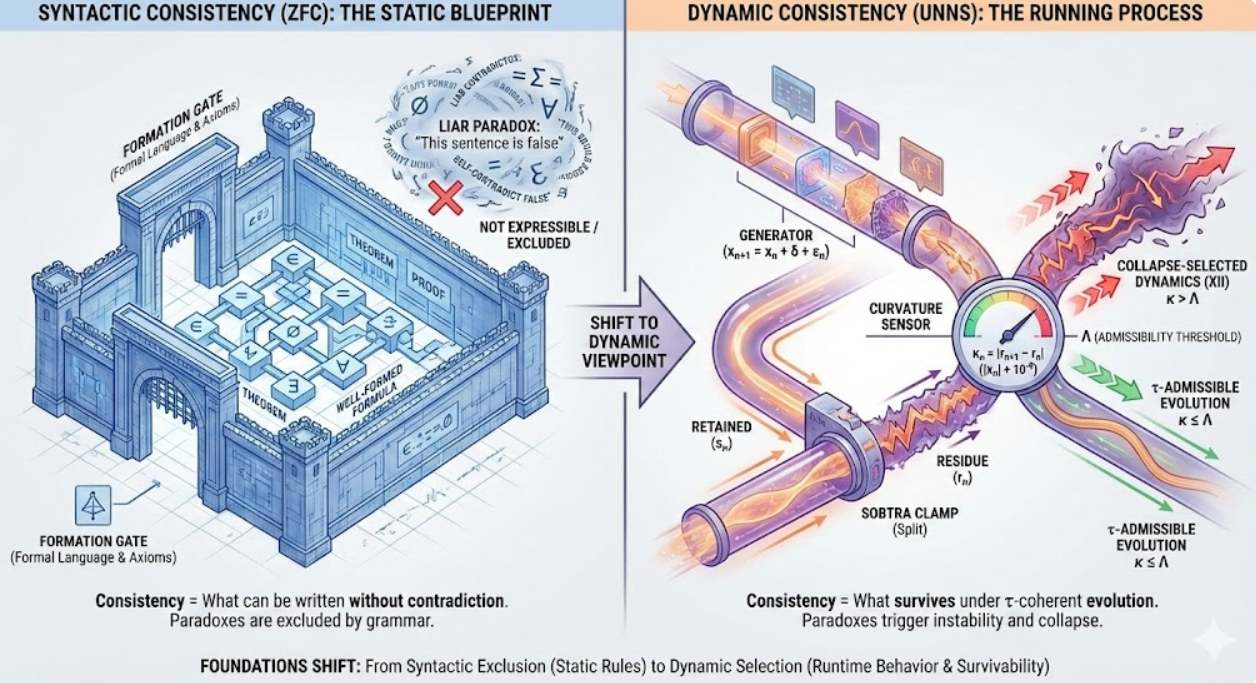
A public, operational viewpoint: what it means to be “consistent” when a mathematical universe is not only axioms, but a running process with admissibility, curvature, and collapse.
Why this article exists
In classical set theory, “consistency” is largely a property of an axiom system and its formal language: what can be written, and what can be proved without contradiction. In UNNS, “consistency” is also a property of behavior: what survives under recursion, what remains admissible under τ-thresholds, and what collapses.
This article does not argue against ZFC. Instead, it clarifies a shift in viewpoint: syntactic exclusion versus dynamic selection. The two approaches can coexist — but they answer different questions.
- Details
- Written by: admin
- Category: UNNS Research
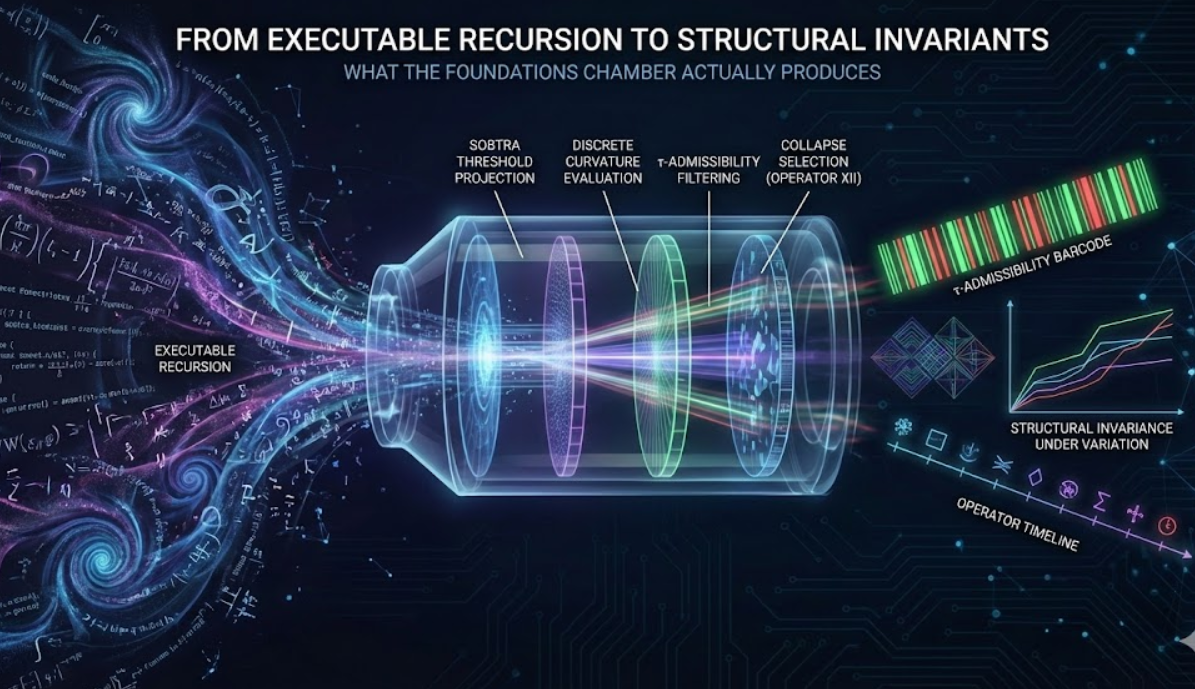
What the Foundations Chamber Actually Produces
Abstract
The UNNS τ-Filtered Observability — Foundations Chamber is not a visualization tool, nor a simulation in the conventional sense. It is an executable instrument designed to extract structural invariants from recursive dynamics under observability constraints.
This article clarifies what kind of results the Chamber produces, how they should be interpreted, and why they are neither numerical constants nor empirical predictions. Instead, the Chamber exposes relations that persist under controlled variation—the defining feature of structural invariants in mathematics and physics alike.

- Details
- Written by: admin
- Category: UNNS Research
Mapping Recursive Structure to the Languages of Science
Introduction
The UNNS Substrate begins with a simple premise:
structure precedes interpretation.
Before equations describe forces, before geometry becomes spacetime, before probability becomes prediction, there exists a deeper layer of organization — a recursive substrate from which formal structures can be constructed, projected, and tested for stability.
- Details
- Written by: admin
- Category: UNNS Research
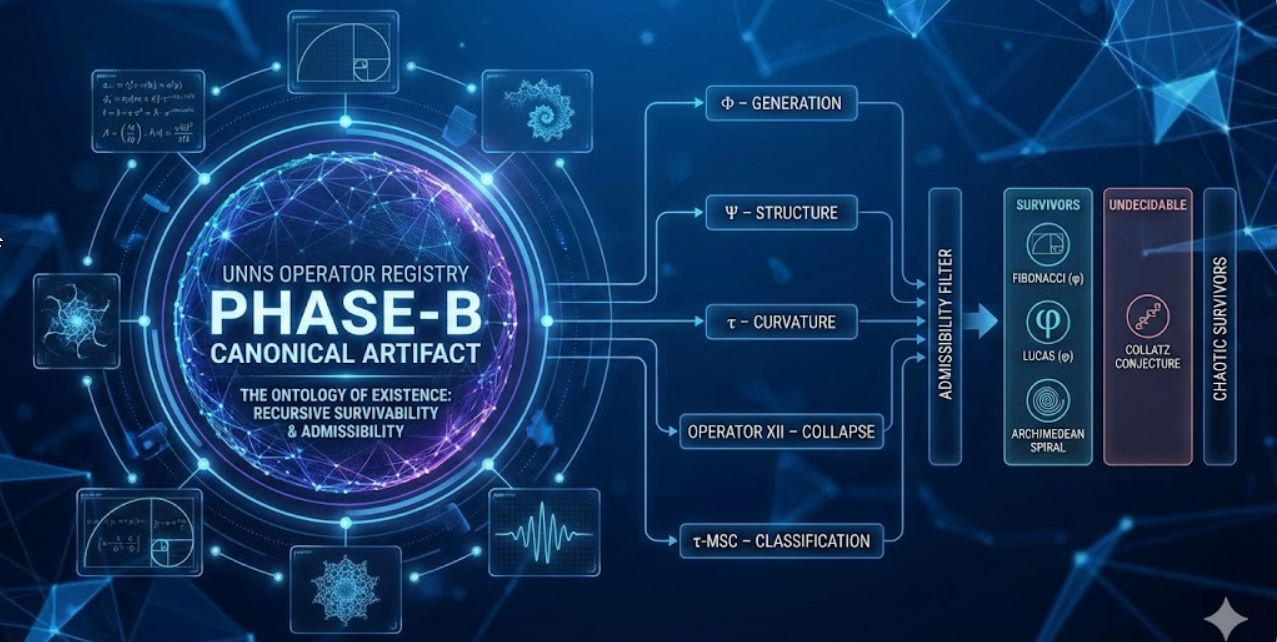
Recursive Survivability as the Defining Criterion of Mathematical Existence in the UNNS Substrate
How recursive survivability defines mathematical existence in the UNNS substrate
In our earlier research article UNNS and the Ontology of Mathematical Existence, we examined longstanding philosophical questions about what it means for mathematical entities to “exist”, and how different ontological positions grapple with that status (e.g., platonism, structuralism, nominalism).philpapers.org
Here we extend those reflections with a concrete artifact: the UNNS Operator Registry, the canonical Phase-B realization of the UNNS substrate.

- Details
- Written by: admin
- Category: UNNS Research
UNNS-Tech Applied to Quantum Mechanics
Abstract
We reinterpret the Born rule — the prescription that the squared magnitude of a wavefunction yields observable “probability” — not as a foundational probability axiom but as the unique surviving invariant under a sequence of UNNS operators. Within the UNNS substrate, ψ itself is a generable recursive structure (Φ-stage). Through structural consistency (Ψ) and curvature stability (τ), |ψ|² emerges as the sole post-collapse invariant admissible under collapse operator XII. This reframes Born’s rule as a consequence of recursive stability and measurement collapse, aligning it directly with outcomes in Chamber XXVI and Chamber XXVIII.
