
- Details
- Written by: admin
- Category: UNNS Research
Unifying Gravitation, Light, Action, and Coupling Through τ‑Field Recursion
Dimensionless Constants → Research τ-Field Geometry UNNS Chambers XIII–XXI τ-MSC v0.9.1 (CaF / SrF / BaF)
Classical physics treats the gravitational constant G, the speed of light c, Planck’s constant ħ and the fine-structure constant α as unrelated inputs: numbers to be measured and inserted into the equations. In the UNNS programme we instead view them as four projections of a single recursion fixed-point of the τ-Field substrate. This article consolidates evidence from the UNNS chambers, τ-field monographs and τ-Microstructure Spectral Chamber (τ-MSC) runs on real molecules to argue that G, c, ħ and α arise from one and the same geometric constraint on recursion.
Abstract
We show how four apparently independent constants — G, c, ħ and α — can be interpreted as different stability channels of a single recursive field (the τ-Field) defined over the UNNS substrate. The argument proceeds in four steps. First, we define τ-curvature wells generated by mass as pacing defects in the recursion cycle and show how conservation of curvature across expanding τ-shells enforces an inverse-square law, fixing an effective gravitational constant G. Second, we recall how Maxwell-FEEC formulations on the substrate identify c as the maximum stable phase-alignment speed of recursion. Third, we review the Tauon Field Information Geometry results in which ħ emerges as the minimal resolvable τ-phase twist times curvature. Fourth, we connect these channels to the transverse torsion stiffness of recursion studied in the dimensionless-constant chambers (XIII–XVIII), where α appears as the stable coupling index for sideways τ-phase propagation.
The core empirical component of the argument is supplied by UNNS Lab experiments: Chambers XIII–XVIII for scale equilibrium and Weinberg angle emergence; τ-MSC Chamber XXI fits to real hyperfine spectra of CaF, SrF and BaF; and cross-validation dashboards verifying that a single τ-Field geometry can account for these seemingly disparate phenomena. Taken together, these results support the claim that G, c, ħ and α form a tightly constrained quadruple determined by a unique recursion fixed-point of the τ-Field substrate.
- Details
- Written by: admin
- Category: UNNS Research
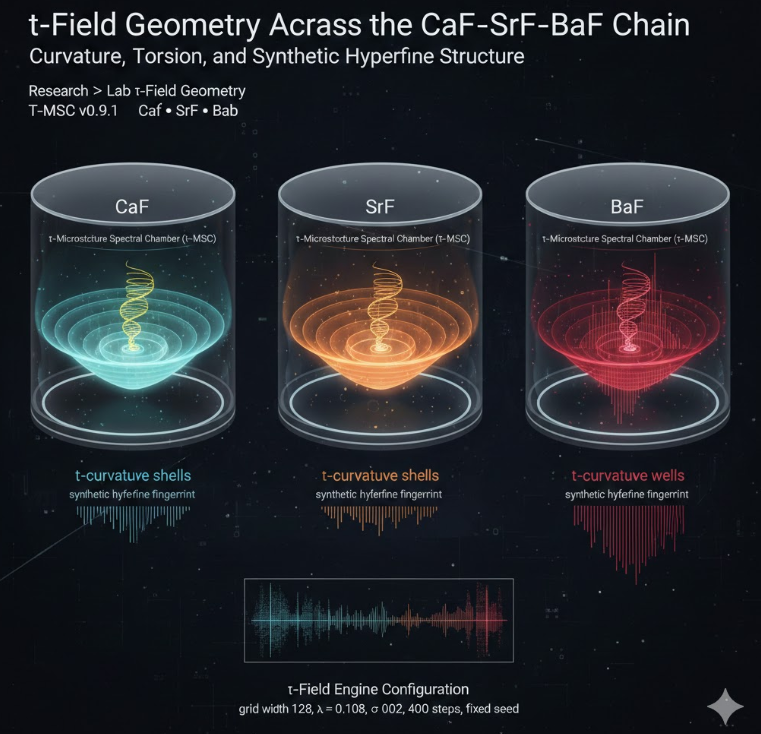
τ-Field Geometry Across the CaF–SrF–BaF Chain — Curvature, Torsion, and Synthetic Hyperfine Structure
Research → Lab τ-Field Geometry τ-MSC v0.9.1 CaF • SrF • BaF
This article reads the CaF–SrF–BaF alkaline-earth fluoride chain through the lens of the τ-Microstructure Spectral Chamber (τ-MSC). Using a single τ-field engine configuration, we fit synthetic τ-MSC spectra to real hyperfine data for CaF, SrF and BaF and interpret the differences as changes in τ-curvature and τ-torsion geometry across the chain.
Abstract
CaF, SrF and BaF share the same electronic ground state (X²Σ⁺, v=0) but differ strongly in nuclear charge and relativistic character. In this study we feed their measured hyperfine transitions into the τ-Microstructure Spectral Chamber and obtain τ-MSC comparison logs for each molecule. All three runs use an identical τ-field engine configuration (grid width 128, λ = 0.108, σ = 0.02, 400 steps, fixed seed), so any differences in the τ-MSC fit arise from how each molecule constrains τ-curvature and τ-torsion in the micro-chamber.
The τ-MSC comparison logs achieve unit match rate for all three species and sub-6 MHz root-mean-square residuals with r² > 0.9999. From these logs we reconstruct qualitative τ-curvature shells, torsion spirals and synthetic hyperfine “fingerprints” for the CaF–SrF–BaF chain. The result is a τ-field geometry narrative that tracks how curvature compresses and torsion tightens as we move from light CaF to heavy BaF.

- Details
- Written by: admin
- Category: UNNS Research
τ-Field Signatures of Heavy-Diatomic Molecules: YbF & SrF as Proto-Unstructured Recursion Objects (UNNS v0.9.1)
Using the χ²-normalized τ-Coupling Engine of UNNS Lab v0.9.1, we confront two workhorse molecules of precision physics — YbF and SrF — with the τ-Field. The result is a new, exploratory picture: these systems behave as hyperfine-silent τ-objects with distinct curvature and τ-phase signatures, despite lacking the manifold structure seen in RaF.
- Details
- Written by: admin
- Category: UNNS Research
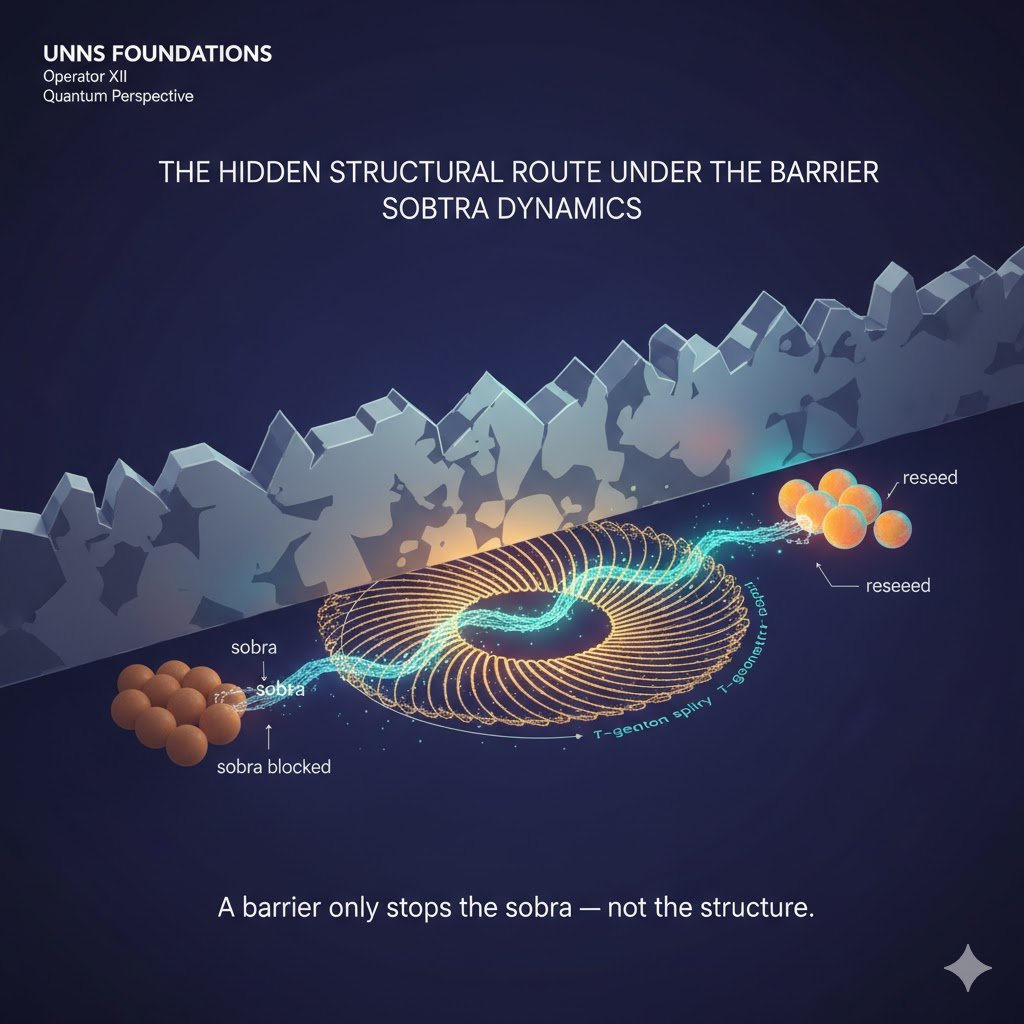
Beyond the Barrier: Why Tunneling Occurs in the UNNS Substrate
In UNNS, a barrier doesn’t stop a structure — it only stops the sobra. When Collapse selects the sobtra channel, the residue follows a torsion-driven micro-route that bypasses classical geometry entirely. This is the structural origin of tunneling.

- Details
- Written by: admin
- Category: UNNS Research
Why the Schrödinger Picture Breaks Down in Field Theory
Quantum Field Theory is usually described as a theory of “operator-valued fields”. In the UNNS substrate, this becomes more precise: the world evolves not by moving states, but by transforming operators and residues. Collapse is the engine, operators are the grammar, and residues carry excitation across the substrate.
