- Details
- Written by: admin
- Category: UNNS Research
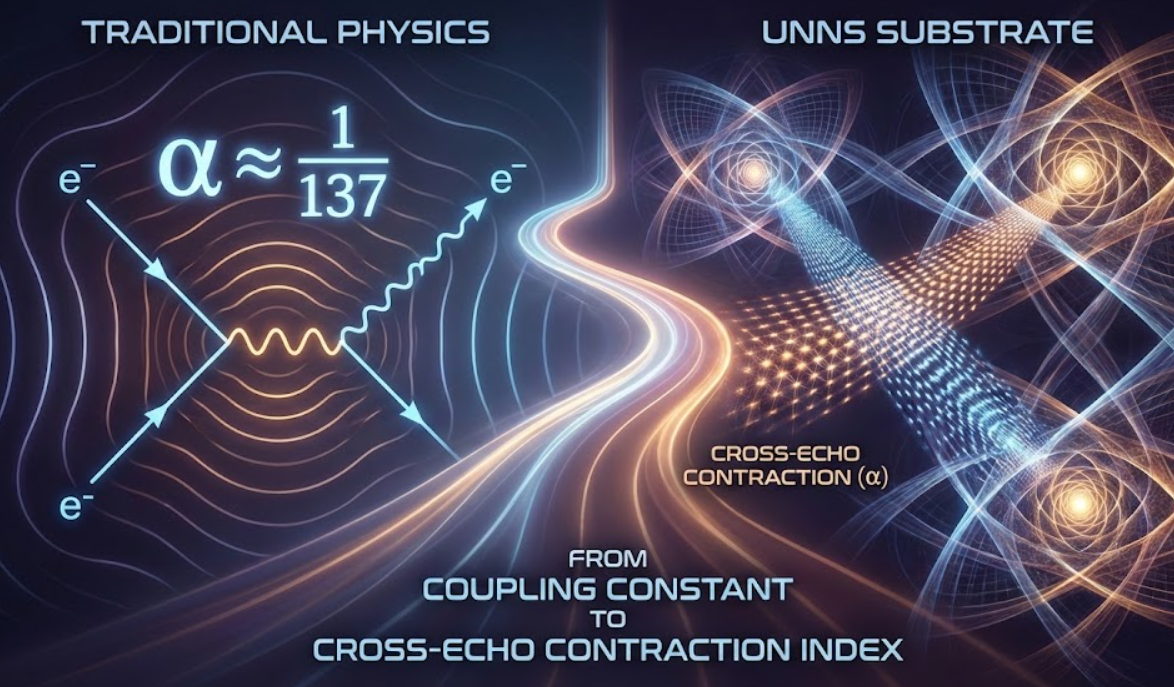
The Fine-Structure Constant in the UNNS Substrate:
From Coupling Constant to Cross-Echo Contraction Index
Foundations → Constants & Invariants UNNS Lab — τ-Field & Echo Channels α in Physics vs α in UNNS
0. Prologue — The Constant That Refuses to Explain Itself
The fine-structure constant α is one of physics’ most enigmatic numbers. It is dimensionless, universal, and appears everywhere the electromagnetic interaction becomes precise. It controls the splitting of spectral lines, the structure of atoms, and the accuracy of quantum electrodynamics (QED), and yet, in standard physics, it is ultimately a given: a number to be measured, not explained.

- Details
- Written by: admin
- Category: UNNS Research
When Two Worlds Meet: Fibonacci, Classical Analysis, and the UNNS Substrate
Foundations → Recursion & Stability UNNS Lab — Chamber Logic Classical vs UNNS
Prologue — Why This Comparison Matters
There are mathematical examples that are trivial in appearance yet structurally revelatory. The Fibonacci sequence is one of them. It has been dissected, analyzed, celebrated, and mythologized for centuries. But what happens when we view it through the UNNS Substrate — a framework that treats recursion not as algebraic coincidence but as a physical flow of echo amplitudes through a computational medium?
This article is a bridge between worlds. It takes a universally familiar mathematical object, the weighted Fibonacci series
S = ∑n=0∞ Fn / 2n,
and shows how two different intellectual traditions — classical analysis and UNNS recursion theory — arrive at the same number but through radically different ontologies. One sees algebraic cancellation; the other sees structural equilibrium. One explains how the sum is computed; the other explains why the sum could not have been anything else.
For the shifted Fibonacci sequence (1,1,2,3,5,...), the sum equals:
S = 4.

- Details
- Written by: admin
- Category: UNNS Research
Collatz, Goldbach, and Gödel in the UNNS Paradox Index
A comparative tour of three iconic problems — Collatz convergence, Goldbach’s even sums, and Gödel’s incompleteness — framed as different faces of recursive instability inside the UNNS Substrate, measured by the UNNS Paradox Index (UPI) and interpreted through Operator XII dynamics. UNNS Paradox Chamber provides the live Collatz–Gödel laboratory where these ideas are made visible.

- Details
- Written by: admin
- Category: UNNS Research
From Localized Hits to Structured Recursions: A τ‑Field View of Quantum Dualism
How the double-slit experiment looks from inside the UNNS Substrate: Φ–Ψ recursion, τ-locks, and why “particle vs wave” was never a true dualism.
Foundations → τ-Field UNNS Lab Context Operator XII Frame
1. The Classical Particle–Wave Dualism Problem
In classical physics, “particle” and “wave” are mutually exclusive categories:
- Particles are localized: they have a position, a trajectory, a hit on a screen.
- Waves are extended: they spread, interfere, diffract through apertures.
Quantum theory famously breaks this separation. In the double-slit experiment:
- The pattern on the detection screen is clearly wave-like: alternating bright and dark fringes (interference).
- Each detection event is sharply localized: a single grain on the screen lights up as if hit by a particle.
The tension is usually presented as a duality: the quantum object is “sometimes a particle, sometimes a wave.” From the UNNS perspective, this phrasing is already a misstep. The object is neither. It is a structured recursion in the τ-Field that projects as particle-like or wave-like depending on how the recursion is sliced and constrained.

- Details
- Written by: admin
- Category: UNNS Research
UNNS Bell Geometry
Why the Gaussian is not statistical but structural — and how Φ, Ψ, and τ carve the Bell shape into the substrate.
How a Bell Curve Works in UNNS
In classical statistics, a Bell Curve (Gaussian distribution) describes how values cluster around a mean, with probabilities shaped by variance.
In UNNS, this picture is reinterpreted entirely through recursion, τ-curvature, and substrate-balance.
The Bell Curve is not a probability curve but a τ-Equilibrium Profile:
a shape that emerges whenever recursive flows stabilize around a minimal-torsion attractor.
Think of it as the static shadow of a dynamic τ-Field.
