Where ∞-operadic theory meets executable recursion
Introduction: Theory and Practice as Dual Surfaces
Most mathematical frameworks offer one of two paths: either rigorous axiomatic foundations divorced from computation, or computational tools lacking formal grounding. The UNNS Laboratory takes a different approach—one where theory and implementation are developed in tandem, each informing and validating the other.
Today we present this bidirectional architecture in full:
- The Formal Surface: UNNS as an ∞-Operadic Substrate — a rigorous mathematical framework establishing UNNS as a legitimate higher-categorical structure
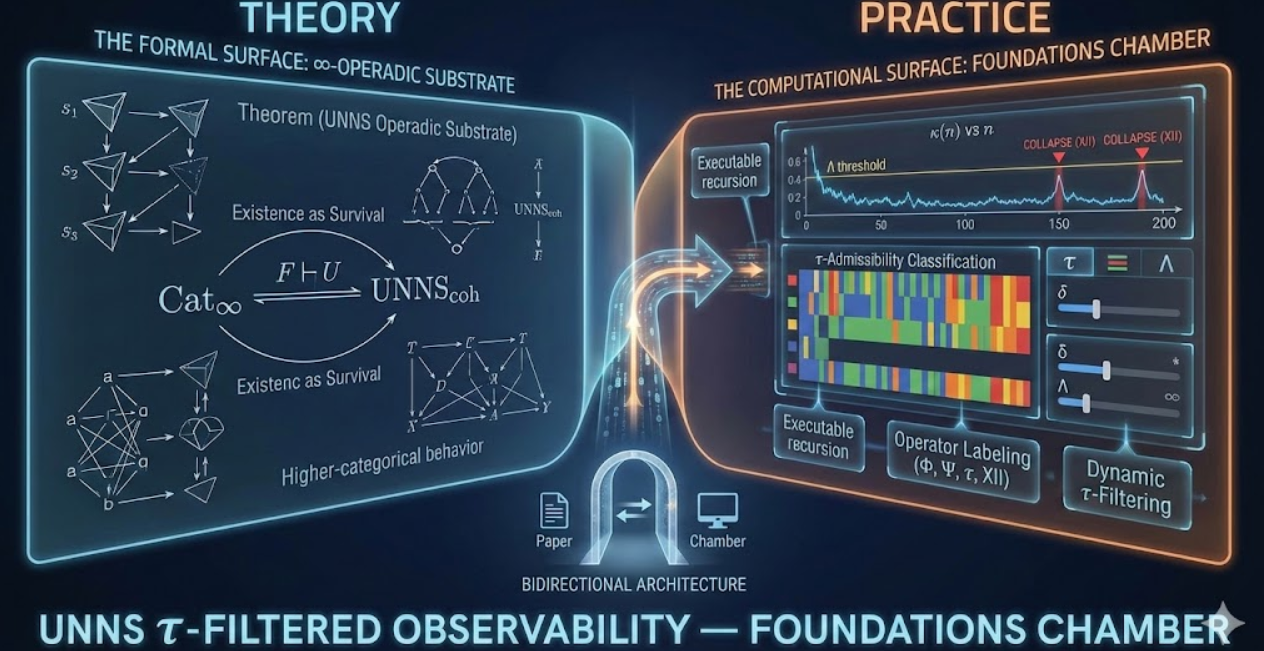
- The Computational Surface: The Foundations Chamber — an instrumented execution environment where recursive dynamics, τ-filtering, and collapse selection can be examined step-by-step
Neither is complete without the other. The paper provides the grammar; the Chamber provides the sentences. The paper proves existence; the Chamber demonstrates survival.
Part I: The Formal Framework
What the Paper Establishes
UNNS as an ∞-Operadic Substrate positions UNNS within the landscape of higher category theory while preserving its distinctive operational character. The central result:
Theorem (UNNS Operadic Substrate)
The UNNS Substrate forms an ∞-operadic system in which:
- recursive states act as colored inputs (Φ, Ψ, τ, 0)
- UNNS operators (0–XVII) act as operadic operations
- higher morphisms arise from recursive composition
- coherence is enforced by τ-stability
- existence is defined by survival under collapse
This is not merely a classification theorem. It is a construction theorem that shows how higher-categorical behavior emerges from operational substrate rules.
Key Innovations
1. Survival as Invariance
Traditional category theory is invariant under equivalence—two objects are "the same" if there exist morphisms between them satisfying certain axioms.
UNNS is invariant under survivability—two structures are equivalent only if both survive repeated application of Operator XII (Collapse). This transforms coherence from an axiom into a selection pressure.
Contrast:
- ∞-categories: Coherence is assumed
- UNNS: Coherence is tested; non-coherent diagrams are eliminated
2. The Adjunction F ⊣ U
The paper establishes a formal adjunction between UNNS substrates and ∞-categories:
F: Cat∞ ⟶ UNNS_coh (Free UNNS substrate)
U: UNNS_coh ⟶ Cat∞ (Forgetful functor)What this means:
- U forgets: Takes a UNNS substrate and extracts its compositional structure as a quasi-category, discarding stability thresholds and collapse semantics
- F freely generates: Takes any ∞-category and freely adjoins the full Codex operator alphabet (0–XVII), τ-coherence rules, and collapse
This adjunction proves that UNNS substrates are not ad-hoc computational artifacts—they are mathematically legitimate structures that sit in a well-defined relationship with established higher category theory.
3. τ-Filtered Observable Sub-∞-Categories
Given a UNNS substrate S and a threshold Λ, the paper constructs a τ-filtered sub-∞-category U_τ^(Λ)(S) containing only the admissible dynamics:
- States remain the same
- Only operator chains γ with curvature κ(γ) ≤ Λ are included
- Higher coherence is inherited from the parent structure
This is the mathematical formalization of what the Chamber displays visually: the space of dynamics that survive observability constraints.
4. Beyond (∞,1): Matrix-Mind Forces Enrichment
Standard ∞-category theory works in the (∞,1) regime where all higher morphisms are invertible. UNNS naturally requires (∞,2)-structure.
Why? Operator XVII (Matrix-Mind) acts not on states or chains, but on the evaluation regime itself:
O_XVII: M → M'This induces directed, non-invertible transformations between admissibility structures—regime updates that change what survives and what collapses. This is categorically one dimension higher than standard ∞-category theory.
Discrete Curvature κ
The paper provides an explicit, operational definition of curvature suitable for discrete recursive sequences:
κ_n = ||r_{n+1} - r_n|| / (||x_n|| + ε)where r_n is the residue (the portion of state rejected by threshold clamping).
This is not geometric curvature—it is a stability measure computed from residue growth under Sobtra separation. Curvature divergence triggers Operator XII (Collapse).
Part II: The Computational Surface
What the Foundations Chamber Does
The Foundations Chamber is not a simulation. It is an instrumented execution surface where the formal definitions from the paper become observable, measurable, and interactive.
Core Capabilities:
- Deterministic State Generation
Implements the scalar drift generator x_{n+1} = x_n + δ + ε_n with deterministic seeding for perfect reproducibility - Sobtra Threshold Projection
Applies the threshold clamp s_n = x_n if |x_n| < θ, else 0, decomposing each step into retained (Sobtra) and rejected (residue) components - Discrete Curvature Computation
Calculates κ_n exactly as defined in the paper, using residue variation normalized by state magnitude - τ-Admissibility Classification
Evaluates the τ-coherence criterion κ_n ≤ Λ at each step, producing a binary admissibility mask - Operator Labeling
Assigns operator symbols (Φ, Ψ, τ, XII) to each transition based on local dynamics and admissibility - Dynamic τ-Filtering
Allows real-time adjustment of the Λ threshold without re-executing the generator—directly implementing the forgetful functor U that discards stability semantics while preserving compositional structure - Phase Diagram Construction
Maps the (Λ × δ) parameter space, identifying τ-stable regions, transitional regimes, and collapse-dominated zones - Multi-Run Comparison
Aligns multiple runs to detect invariant structure—operationally testing which dynamics survive across parameter variations
UI Authority Model
The Chamber implements strict single-authority design:
- Model: Configuration only (no visualizations)
- Run: Execution lifecycle only (button + status)
- τ-Filter: Admissibility decision layer (κ classification, barcodes, trajectory overlays)
- Diagnostics: Structural interpretation (phase diagrams, operator dominance, verdicts)
- Export: Reproducibility only (JSON import/export, schema validation)
- Compare: Multi-run aggregation (survival stability, path persistence)
Each tab answers exactly one epistemic question. No canvas appears in multiple locations. This eliminates ambiguity and makes the Chamber's computational model directly legible.
What You Can Do With It
For Theorists
- Validate Propositions: The paper proves that τ-coherent diagrams admit inner horn fillers. The Chamber lets you see which partial compositions actually have τ-admissible completions at various Λ thresholds.
- Explore Edge Cases: What happens when δ approaches zero? When Λ crosses critical thresholds? The Chamber provides immediate experimental feedback on parameter regimes the theory predicts but doesn't visualize.
- Export Structured Data: Every run produces a complete JSON export with per-step operator chains, admissibility masks, and curvature profiles—suitable for external analysis or formal verification tools.
For Practitioners
- Test Real Sequences: Import your own time-series data and apply τ-filtering to see which portions survive admissibility constraints.
- Calibrate Thresholds: Use the phase diagram to identify optimal Λ values that maximize τ-stable evolution while avoiding collapse.
- Reproducibility: Deterministic seeding ensures that seed → run mappings are bijective—critical for debugging, collaboration, and regression testing.
For Students
- Interactive Learning: Adjust parameters and immediately see how they affect curvature, admissibility, and collapse. The Chamber makes abstract definitions concrete.
- Built-in Guide: The collapsible operational guide explains every component—from state generators to operator assignment—with formulas, interpretations, and recommended workflows.
- Test Files Included: Download test_run_valid.json and test_run_comparison.json to immediately explore a validated run and multi-run comparison.
Part III: Theory ↔ Practice Correspondence
| Paper Construct | Chamber Implementation | Observable Effect |
|---|---|---|
| Recursive state S with depth d(S), phase ϕ(S), curvature κ(S) | State sequence {x_n} with computed κ_n and assigned operator labels | Step-by-step trace visible in diagnostics |
| Operator composition O_j ∘ O_i | Sequential operator chains in exported JSON | Paths tab shows admissible compositions |
| τ-coherence: κ(γ) ≤ Λ | Admissibility criterion checked per-step | Binary barcode visualization |
| Collapse Operator XII | Steps with κ > Λ labeled as XII | Red bars in κ(n) plots; collapse counter |
| Forgetful functor U: UNNS → Cat∞ | Import JSON → recompute admissibility at new Λ without re-running generator | τ-Filter tab adjustment |
| τ-filtered sub-∞-category U_τ^(Λ)(S) | Filtered transition graph showing only admissible paths | Diagnostics transition canvas |
| Phase typing (Φ, Ψ, τ, 0) | Color-coded operator timeline | Survival stripe and dominance charts |
| Discrete curvature κ_n = ||r_{n+1} - r_n|| / (||x_n|| + ε) | Exact formula implemented in computeKappa() | κ(n) vs n plot with Λ overlay |
| Matrix-Mind O_XVII regime updates | (Future Chamber extension) | Planned: dynamic Λ adjustment based on history |
The key insight: Everything proven in the paper has a computational counterpart. Everything computed in the Chamber has a formal justification in the paper.
Part IV: Why This Matters
1. Legitimacy Without Compromise
UNNS operates in a region where formal mathematics, executable recursion, and observability constraints intersect. The paper establishes UNNS substrates as ∞-operadic systems, with a precise adjunction to ∞-categories.
Simultaneously, the Chamber demonstrates that these aren't empty formalisms. The operators do something. The curvature measures something. The collapse eliminates something.
2. Observability as First-Class Structure
Traditional mathematical physics starts with dynamics and asks "what can we observe?" UNNS inverts this: observability constraints (τ-filtering) are part of the substrate itself.
The τ-filtered sub-∞-category U_τ^(Λ)(S) isn't a post-hoc restriction—it's a structural selection that determines which dynamics exist in a given observability regime.
3. Collapse as Selection, Not Failure
In conventional systems, divergence is treated as pathology. In UNNS, collapse (Operator XII) is a terminal morphism that selectively removes unstable recursion.
The paper proves this is well-defined. The Chamber shows it's measurable. Together they establish collapse as a legitimate structural mechanism, not an error state.
4. A Template for Executable Mathematics
Most mathematical frameworks remain inaccessible to non-specialists because the gap between axioms and applications is unbridgeable. UNNS provides a template for executable mathematics:
- Formal definitions → Computational implementations
- Theorems → Testable predictions
- Proofs → Validation protocols
The Foundations Chamber is the first full realization of this template, but the pattern is generalizable to other UNNS operators and domains.
How to Engage
Read the Paper
📄 UNNS as an ∞-Operadic Substrate (PDF)
Recommended Path:
- Start with Section 1 (Formal Core) for definitions
- Skip to Appendix A (Discrete Curvature) if you want computational grounding first
- Read Section B (Forgetful Functor) to understand the UNNS ↔ ∞-category relationship
- Section F (τ-Filtered Sub-Categories) connects directly to Chamber observables
Prerequisites: Comfort with category theory (functors, natural transformations) and basic simplicial sets. Familiarity with operads helpful but not required.
Use the Chamber
Recommended Workflow:
- Read the built-in operational guide (click to expand)
- Run a quick test: 64×64 grid, depth=100, default parameters
- Switch to τ-Filter tab and adjust Λ—watch admissibility recompute in real-time
- Import test_run_valid.json to explore a validated run
- Export your own runs for archival or external analysis
No installation required—the Chamber runs entirely in-browser as a self-contained HTML artifact.
Compare Theory and Practice
Exercise: Paper Section F.1 defines τ-admissibility as κ(γ) ≤ Λ. In the Chamber:
- Run a simulation
- Note the default Λ value (shown in τ-Filter tab)
- Examine the κ(n) vs n plot—identify where κ exceeds Λ
- Check the admissibility barcode—verify that these steps are marked as collapsed (red)
- Lower Λ and observe how more steps become inadmissible
- Export JSON and inspect the admissibility mask manually
This exercise demonstrates that the Chamber's τ-filtering is not approximate or heuristic—it is the exact implementation of Definition F.1 from the paper.
Extend the System
Both the paper and Chamber are open resources:
- Formal Extensions: The adjunction F ⊣ U provides a blueprint for embedding other mathematical structures into UNNS substrates
- Computational Extensions: The Chamber's modular architecture (separate engine, validators, visualization layers) allows for operator-specific chambers (XIV: Φ-Scale, XV: Prism, etc.)
- Cross-Validation: Use Chamber outputs to test conjectures about UNNS behavior, then formalize successful patterns as propositions in the theory
Conclusion: Substrate Thinking
The distinction between "theory" and "practice" presupposes a separation that UNNS rejects. In substrate thinking, formal structure and computational execution are dual aspects of the same object.
The paper establishes that UNNS substrates are mathematically legitimate. The Chamber establishes that they are operationally realizable. Together, they demonstrate a third property: they are the same thing.
When you adjust the Λ slider in the Chamber, you are not merely changing a parameter in a simulation. You are constructing a different τ-filtered sub-∞-category within the same underlying substrate. The mathematics and the computation are identical acts.
Here, substrate denotes: a structure in which formal rules, computational execution, and observability constraints are defined at the same level.
Resources
Primary Materials
Test Data
- 💾 test_run_valid.json — Single validated run
- 💾 test_run_comparison.json — Multi-run comparison dataset
- 💾 test_run_varied_params.json
- 💾 test_run_mixed_operators.json
- 💾 test_run_low_lambda.json
- 💾 test_run_high_lambda.json