UNNS Visual Engine

Details
Written by: admin
Category: Labs

Invariants of recursion

Substrate Instrument — Operator Laboratory (Φ–Ψ–τ–XII) with τ-Flow Evolution

Scope Exploration Tool Phase τ-Flow / Phase-F Outputs Invariants + JSON Logs Modes 2D · τ-Geometry 3D · Collapse View
Open Full Window (Default) Embedded Instrument How to Read It
Interpretation: The UNNS Visual Engine produces mathematically defined structures, operators, and invariants within the UNNS substrate. Mathematical interpretation is intrinsic to the framework. How these results are further interpreted — heuristically or in relation to external domains — is left to the researcher.

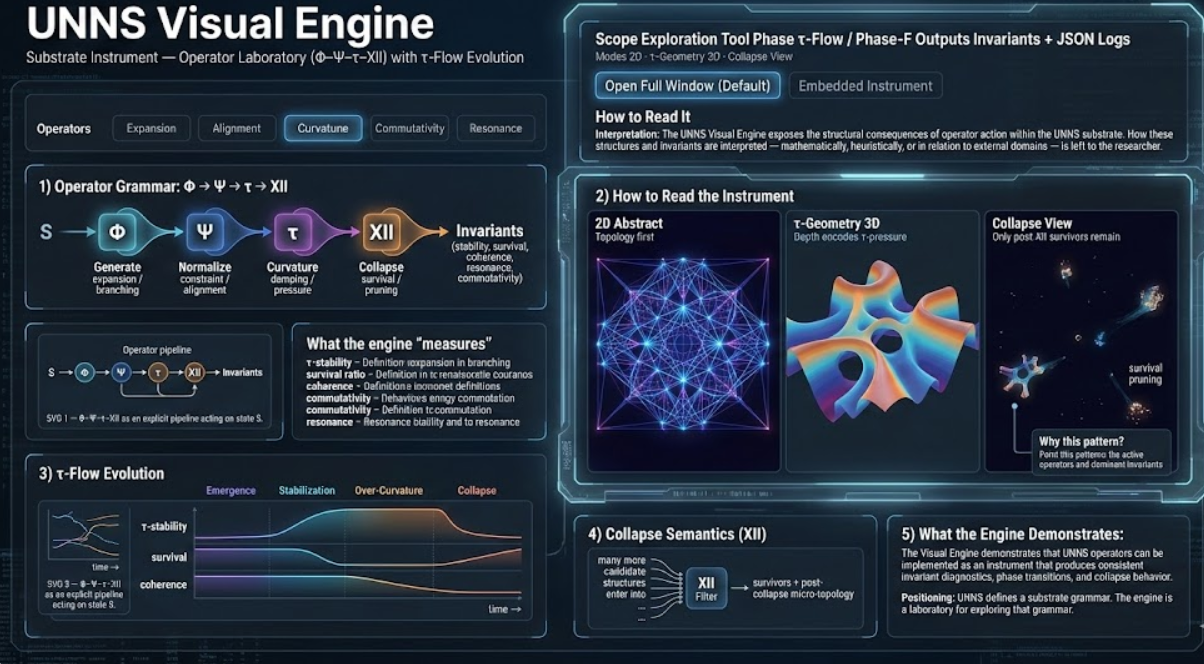
1) Operator Grammar: Φ → Ψ → τ → XII

The engine treats recursion as an operator process. Each operator transforms the current state, and the observable quantities are invariants (stability, survival, coherence, resonance, commutativity) rather than raw numbers.

Operator Pipeline State is transformed by operators; invariants are measured after each step. Seed / State S values[], entropy, curvature, depth operatorTrace, collapsed Φ Generate expansion / branching Ψ Normalize constraint / alignment τ Curvature damping / pressure XII Collapse survival / pruning Key idea: the observable is not the number — it is the invariant profile produced by operator action.
Fig. 1 — Φ–Ψ–τ–XII as an explicit pipeline acting on state S. Operator Pipeline State is transformed by operators; invariants are measured after each step. Seed / State S values[], entropy, curvature, depth operatorTrace, collapsed Φ Generate expansion / branching Ψ Normalize constraint / alignment τ Curvature damping / pressure XII Collapse survival / pruning Key idea: the observable is not the number — it is the invariant profile produced by operator action.

What the engine measures

  • τ-stability: damping balance (variance before vs after τ)
  • survival ratio: fraction surviving XII
  • coherence: smoothness of recursive differences
  • commutativity: sensitivity to operator order
  • resonance: harmonic alignment / periodic structure

2) How to Read the Instrument

Treat the visualization as a projection. The meaning lives in invariants, phase changes, and the collapse boundary.

Projection Modes Same state; different observation lenses. 2D Abstract Topology first. No τ-depth. τ-Geometry 3D Depth encodes τ-pressure. Collapse View Only post-XII survivors remain. Projection Modes Same state; different observation lenses. 2D Abstract Topology first. No τ-depth. τ-Geometry 3D Depth encodes τ-pressure. Collapse View Only post-XII survivors remain.
Fig. 2 — Three projections: 2D, τ-depth, and post-collapse survivors.

The “Why this pattern?” panel is the interpretation bridge: it explains the current regime using the active operators and dominant invariant.

Embedded Instrument

The engine is embedded below. For the intended lab experience, use Open Full Window (Default) at the top.

Open Full Window  Open Guide Module

3) τ-Flow Evolution

τ-Flow evolves the state over discrete steps by reapplying the operator stack. This reveals phase changes: emergence → stability → over-curvature → collapse.

τ-Flow Evolution Phases + invariants (conceptual schematic). Emergence Stabilization Over-Curvature Collapse time → τ-stability survival coherence XII triggers
SVG 3 — τ-Flow as phased evolution (schematic): invariants drift, then collapse boundary appears.

4) Collapse Semantics (XII)

Collapse is not a visual “effect”. It is an operator boundary that filters structure. In Collapse View, sparsity is expected: it means XII was strong.

XII — Collapse as a Filter Many candidates enter; only survivors remain. XII Filter survival pruning Collapse View shows the right-hand structure: survivors + post-collapse micro-topology.
SVG 4 — Collapse as a structural filter: not every recursive structure remains viable under XII.

Exported JSON captures operator trace, invariants, and (when τ-flow is active) phase changes and events — making runs reproducible and comparable.

5) What the Engine Demonstrates

The Visual Engine demonstrates that UNNS operators can be implemented as an instrument that produces consistent invariant diagnostics, phase transitions, and collapse behavior. 

Positioning: UNNS defines a substrate grammar. The engine is a laboratory for exploring that grammar.

6) Significance of the Visual Engine

The UNNS Visual Engine is significant not because it visualizes recursion, but because it makes operator invariants observable as first-class objects. In classical mathematics, invariants are often introduced only after a structure is fixed. Here, invariants arise dynamically from operator action itself.

This shifts the role of recursion from a procedural mechanism to a substrate process with measurable regimes. Stability, collapse, resonance, and commutativity are no longer abstract labels; they become directly inspectable features of recursive evolution.

By implementing Φ, Ψ, τ, and XII as an executable operator grammar, the engine demonstrates that recursive systems admit phase structure: emergence, stabilization, over-curvature, and collapse. These phases are not imposed externally, but follow from invariant behavior.

The significance of the engine therefore lies in its role as a boundary object: it connects formal operator definitions, invariant mathematics, and exploratory investigation within a single coherent instrument.

In short: the Visual Engine shows that UNNS recursion is not merely iterable, but classifiable, phase-bearing, and structurally constrained by its own invariants.

Main Menu