Ordering Noise, Dynamic Completion, and the Universality of Least-Divergence Selection
validation of dynamic behavior in the refinement process · σ-robustness · Mode B ordering noise · discrete cost quantum transition · reproducible sweeps
Why this moment matters
Most speculative frameworks never reach the point where they can be challenged by controlled perturbations and still remain coherent. Chamber XXXI (check for more here) is explicitly built to do the opposite of “demo culture”: it tries to break the mechanism.
- It perturbs the process along independent axes (decision noise vs ordering noise).
- It forces reproducibility (σ=0 determinism) and statistical aggregation (σ-sweeps).
- It exposes failure modes as measured diagnostics — not as narrative excuses.
The result is a clean transition point: from “patching to keep the story alive” to extension driven by measurable invariants.
Key findings (what the chamber actually demonstrated)
1) σ=0 determinism is exact.
The baseline run is perfectly reproducible: identical seed → identical exploration trace → identical minima.
2) Ordering noise (Mode B) is a real perturbation axis.
Costs and admissibility remain unchanged; only the exploration order of cost-comparable edits is perturbed.
3) Discrete cost quantum is not a nuisance; it is a structural scale.
When costs are quantized, a robust scale estimator can collapse (MAD≈0). Chamber XXXI detects this and
interprets σ directly in units of the cost quantum.
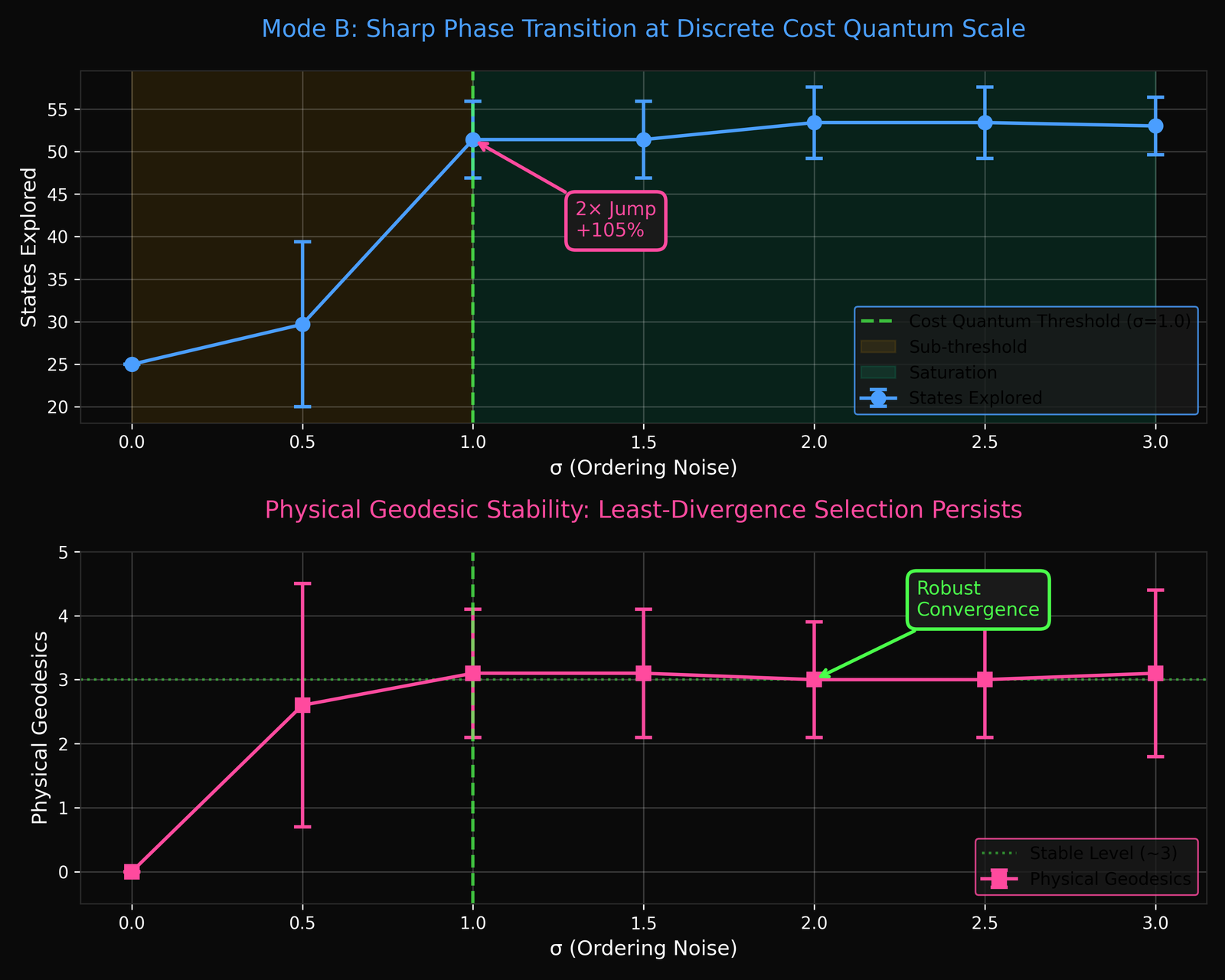
4) A sharp phase transition appears at σ≈1.0 (cost quantum threshold).
Below σ≈1.0, ordering permutations are locally constrained; at σ≈1.0, adjacent cost classes become permutable,
unlocking a larger exploration volume.
5) Least-divergence selection persists.
Even when exploration volume expands (often dramatically), physical geodesics (least-divergence endpoints)
remain stable — indicating the principle is not an artifact of exploration order.
What this upgrades, scientifically
In *The Dynamic Completion of the UNNS Substrate*, we established robustness of least-divergence selection under decision-level perturbations, where stochasticity modifies the evaluation of candidate refinements. *Ordering Noise and the Universality of Least-Divergence Selection in the UNNS Substrate* subjects the theory to a more stringent test by examining whether its core results remain stable when the order of exploration itself is perturbed.
- Decision noise: “What if costs are uncertain?”
- Ordering noise: “What if the search explores ‘equally good’ edits in a different order?”
If least-divergence were merely a heuristic effect, Mode B should have changed the outcome. Instead, it changes how the system explores — without changing what it converges to.
Mode B validation snapshot
The measured signature: a sharp exploration transition at the discrete cost quantum scale (σ≈1.0), while physical geodesics remain stable (least-divergence selection persists).
Two independent perturbation axes
Chamber XXXI separates two ways to “stress” refinement dynamics: (A) perturbing decisions (cost evaluation) and (B) perturbing ordering (exploration history). Mode B is intentionally conservative: it permutes within cost tie-bands without destroying global ordering.
Mode B in one diagram: tie-band permutation
Mode B does not “randomize the search.” It performs a minimal perturbation: it only permutes edits inside local cost bands, while preserving the global cost ranking. This is the cleanest ordering-noise model that avoids destructive randomness.
Significance: what Chamber XXXI really “proved” in practice
Chamber XXXI does not claim that a single algorithm is “correct.” It does something stronger: it shows that a specific selection mechanism (least-divergence geodesics) remains stable under perturbations that would normally invalidate heuristic conclusions.
Universality (scoped): within the UNNS refinement substrate, once exploration is sufficiently complete, least-divergence endpoints behave like an attractor: the system can explore differently, yet converge to the same physical structure.
Discrete cost quantum as a structural constant: σ≈1.0 is not an arbitrary tuning point. It is the scale where ordering permutations can cross cost levels. That’s why the transition is sharp and reproducible.
Extension-ready state: the chamber now supports the next step: moving from “qualified universality” to “strong universality” by testing broader grammars, deeper regimes, and metric families — without changing the validation core.
How to use Chamber XXXI (practical)
- Open the chamber and run σ=0 once to confirm determinism.
- Run a σ-sweep in Mode B to observe the cost-quantum threshold behavior.
- Export JSON sweep data for archiving and paper-level aggregation.
- Switch mass definitions (m₁/m₂/m₃) to test invariance across structural measures.
No JS is required on the article side; the chamber itself is the interactive environment.
What to read (paper pairing)
- The Dynamic Completion of the UNNS Substrate — establishes the completion/validation framing and the refinement-geodesic lens.
- Ordering Noise and the Universality of Least-Divergence Selection — proves the second perturbation axis and the σ≈1.0 transition.
From here on, it’s extension — not repair
A chamber earns that statement only when it has survived a deliberate attempt to falsify its core claim, while still producing diagnostics sharp enough to guide the next experiments.
Chamber XXXI reached that point: it perturbed both decision and ordering, detected discrete-cost structure, revealed the σ≈1.0 transition, and still preserved least-divergence selection as a stable outcome.
