What Matter Really Is in the UNNS Substrate: From τ-Curvature to Closure Dynamics
Foundations UNNS Substrate τ-Field · Closure
Why “Matter” Needs a New Definition
In standard physics, matter is usually defined by its behaviour: it has mass, it occupies space, it follows quantum rules, it curves spacetime. Every theory describes these behaviours differently, but all of them quietly assume there is some “stuff” underneath.
The UNNS Substrate takes a different route: there is no stuff underneath. There is only a recursion engine acting on Nests. Geometry, fields and particles are projections of that recursion.
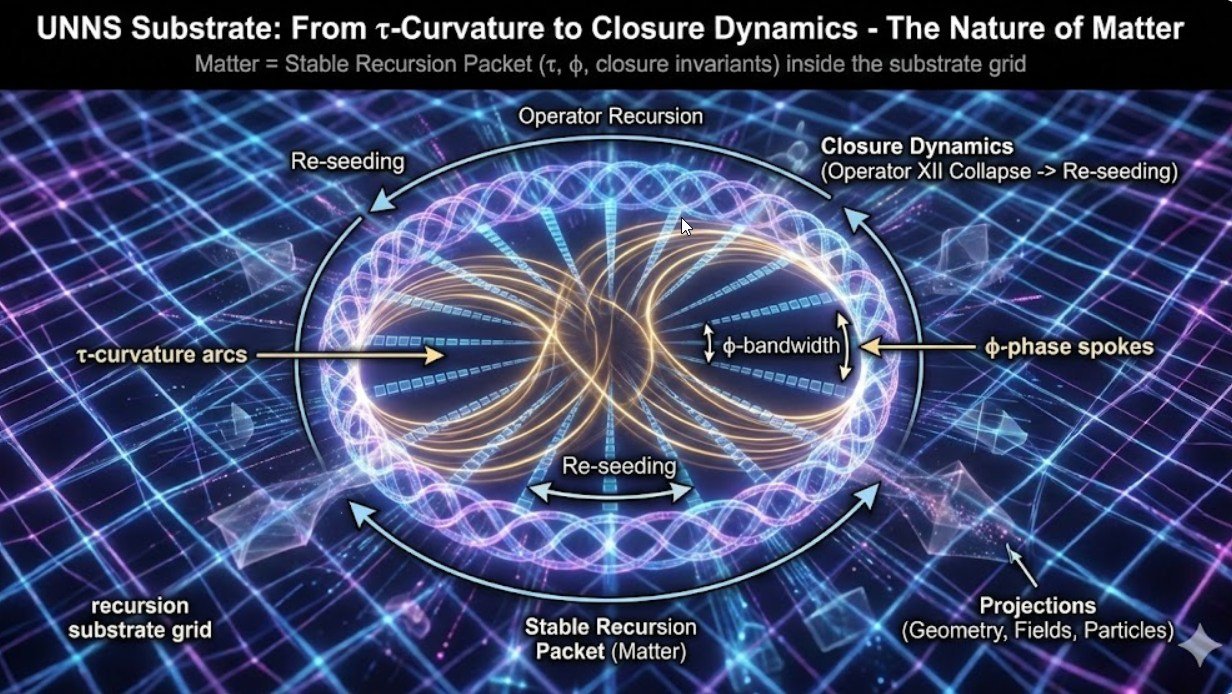
In this view, matter is not a substance. It is a stable recursion packet with characteristic τ-curvature, φ-bandwidth and closure dynamics.
1. The Substrate: No “Stuff”, Only Recursion
UNNS starts with a simple but radical move: there is no fundamental substance. The base layer of reality is a recursion substrate:
- Operators act on Nests, generating new structure.
- Each step produces a new configuration of τ-curvature, φ-phase, closure and residue.
- Geometry, fields, particles and even “time” are projections of this activity.
At this level, nothing is “made of” anything else. There are only patterns of recursion and the invariants they maintain.
2. Matter = Stable Recursion Packet
In this substrate, matter is a special kind of pattern: a stable recursion packet.
A recursion packet is a region of the substrate where:
- τ-curvature remains within a narrow band (τmin to τmax).
- φ-phase is organised into a discrete φ-bandwidth rather than random noise.
- closure cycles repeat under Operator XII collapse without dissolving.
- residue density and torsion events settle into a repeatable pattern.
When such a packet survives many substrate steps, we perceive it as a particle, a field excitation or a molecule depending on scale and projection.
3. τ-Curvature: Why Matter Has Mass
τ-curvature is UNNS’s internal measure of how strongly a Nest is being bent by recursion. When τ is low, the substrate is relaxed; when τ is high, the Nest is under strain.
A matter packet is one where the τ profile is:
- smoothly increasing with depth (no chaotic spikes),
- bounded above by a finite τmax,
- resilient under Operator XII collapse (the strain pattern regrows after each cycle).
In projection:
- in quantum theory this appears as rest energy,
- in GR it appears as mass–energy density that curves geometry.
From the substrate’s point of view there is no “mysterious mass field”. Mass is simply resistance of a recursion packet to τ-deformation.
4. φ-Bandwidth: Why Matter Has Charge and Phase
Every recursion packet also has a characteristic distribution of φ-phase. Instead of being spread randomly, the phases occupy a discrete φ-bandwidth.
This bandwidth controls:
- how the packet interferes with other packets,
- which gauge symmetries it respects,
- how it responds to phase shifts from external fields.
When projected into quantum theory, these properties appear as:
- electric charge (phase winding around loops),
- spin (structured phase on internal cycles),
- internal quantum numbers such as flavour and colour.
Thus, in UNNS, charge and spin are not extra labels; they are phase-geometry features of the recursion packet.
5. Closure Dynamics: Why Matter Persists
Closure is the substrate’s way of asking: “Does this recursion eventually give me back the same Nest?”
For a generic pattern, Operator XII (collapse) and subsequent steps destroy structure. The Nest fails to close; residue spreads; torsion events scatter information.
A matter packet is precisely a pattern where:
- the recursion loop closes to within small tolerance,
- residue density remains bounded in each cycle,
- torsion events recur in a characteristic sequence.
In projection, this looks like a particle that:
- has a long lifetime or is stable,
- has sharply defined quantum numbers,
- can be created and annihilated in consistent channels.
Matter is what survives collapse. Everything else is transient substrate foam.
6. Interactions: When Packets Share Recursion History
In UNNS, interactions between pieces of matter are not “forces” transmitted by abstract fields. They are overlaps of recursion packets.
- When τ-curvature profiles interact, we see gravitational effects and mass–energy exchange.
- When φ-bandwidths interlace, we see gauge interactions (EM, weak, strong).
- When closure cycles splice and rejoin, we see particle reactions and decay chains.
The familiar “force carriers” of the Standard Model correspond to special recursion packets whose main role is to rephase or re-wire other cycles rather than to store mass.
7. How This Reframes Standard Physics
7.1 Quantum Mechanics
Wavefunctions and operators are shadows of the substrate’s recursion rules. A “particle” in QM is simply the projection of a recursion packet into Hilbert space. Superposition and interference are what φ-bandwidth looks like when viewed through this projection.
7.2 Quantum Field Theory
Fields become effective descriptions of τ and φ distributions over many Nests. Creation and annihilation operators are coarse-grained views of closure cycles starting and ending.
7.3 General Relativity
Spacetime curvature is the geometric shadow of τ-curvature averaged over large regions of the substrate. “Matter tells spacetime how to curve” is just another way of saying recursion packets strain the τ-field and that strain looks geometric.
8. Summary: What Matter Really Is
- The universe’s base layer is a recursion substrate, not a field of substances or a pre-existing geometry.
- Matter is a stable recursion packet: a pattern of τ-curvature, φ-bandwidth and closure cycles that survives collapse and re-seeding.
- Mass is resistance to τ-deformation, charge and spin are structured phase geometry, and stability is successful closure.
- Forces, fields and spacetime are projections of how these packets interact and strain the substrate.
In this sense, matter is not what the universe is “made of”. Matter is how the universe’s recursion chooses to remember itself.