Reality Without Observers

Details
Written by: admin
Category: UNNS Research

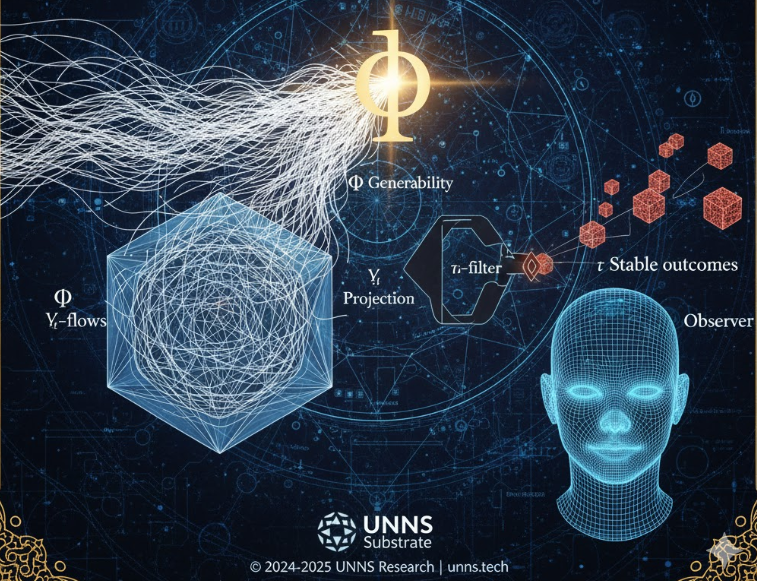
Persistence, Generability, and Stability in the UNNS Substrate

Substrate Ontology · Φ–Ψ–τ Clarification · Structural Testability

Theme Substrate Ontology Focus Φ–Ψ–τ Mode Conceptual Clarification

Introduction

The observer debate in quantum foundations often collapses into a false binary: either observers "create" reality, or reality exists in a fully classical sense without any dependence on interaction. The UNNS Substrate offers a third position: reality exists independently of minds, while still being filtered into persistence by stabilization mechanisms that are physical, not psychological.

This follow-up article is a structured response built around three critical discussion points: (1) the Persistence Problem, (2) defining Φ without collapsing it into Ψ, and (3) the Testability Gap. It is written in the light of two formal UNNS foundation papers:

1. The Persistence Problem (Pre-Life Universe)

A common objection appears immediately once observers are removed: If Φ exists before observers, but τ (stable reality) requires an observer's filter, what happened in the billions of years before life?

The UNNS-consistent move is to de-anthropomorphize the concept of an "observer" completely. In UNNS terms:

  • Observer ≠ consciousness
  • Observer ≠ agent
  • Observer = τ-capable interaction

The refined statement becomes precise:

τ-stability does not require observers; it requires irreversible interaction.

This matters because it dissolves the false historical paradox. A rock, a molecule, a star, a dust grain: each already functions as a τ-filter. Decoherence, dissipation, and record formation are sufficient. Conscious observers are not ontological prerequisites; they are high-order τ-interfaces.

Therefore the pre-life universe was not "unstable." It was:

  • rich in Φ-generability,
  • continuously undergoing Ψ-interaction,
  • producing τ-stable structures through matter–matter interactions.

Life adds recursive modeling, not existence.

One-line refinement: τ is not triggered by observation, but by interaction that exceeds a survivability threshold.
Big Bang Φ emerges First stars τ-stability Planets form τ-complexity Life emerges τ-modeling Φ Ψ τ Reality persists before observers

2. Defining Φ Without Collapsing It Into Ψ

This is the hardest point, and it is where careless language destroys the whole proposal. If Φ is described too loosely, critics will respond:

"You've just renamed the wavefunction."

The distinction must therefore be sharpened and made explicit. A clean way to state it:

Aspect Ψ (QM) Φ (UNNS)
Ontological status State of a system Pre-system generative field
Mathematical role Amplitude over configurations Rule-space of configuration generation
Evolves in time? Yes Not necessarily (atemporal or meta-temporal)
Defined on Hilbert space? Yes No (Ψ emerges from Φ)
Carries probabilities Yes No (probability emerges at τ)

The single sentence that must be emphasized:

Φ is not a state of anything. It is the space of possible state-generation rules.

That sentence separates UNNS from:

  • hidden-variable theories,
  • pilot-wave theories,
  • Everettian "one-Ψ" realism.

A safe analogy (non-mystical, purely structural):

  • Ψ is a function.
  • Φ is the grammar that generates functions.

Not the wave — the language waves are written in.

Φ-Regime Generative Grammar Ψ₁ Ψ₂ Ψ₃ Generated states Multiple wavefunctions from single generative structure

2.1. Mathematical Formalism of Φ-Generability

The Phi-Regime paper introduces a generator mapping that makes the distinction concrete. Here we unpack the key formal structures:

Gen : Φ → F(H(C))

For each φ ∈ Φ:
Gen(φ) = {Ψₖ | k ∈ K}

This formulation encodes three critical features:

  • Non-embedding: φ is not an element of H(C)
  • Family generation: A single φ generates multiple Ψ structures
  • Context-dependence: Index k encodes boundary conditions, recursion depth, or measurement context
Φ (Law-space) φ₁ φ₂ Gen F(H(C)) Ψ₁ Ψ₂ Ψ₃ Ψ₄ Ψ₅ State-space (projectable)

The generator map produces families of states from non-state structures

3. The Testability Gap (Where UNNS Must Earn Its Keep)

The "holy grail" question is unavoidable: how does one distinguish a UNNS substrate claim from an interpretation that merely rewords Copenhagen?

Here restraint matters. What should not be claimed:

  • Do not claim UNNS already beats Copenhagen experimentally.
  • Do not claim "Φ-resonance" is obvious in existing data.

What can be claimed legitimately is sharper and more defensible:

UNNS predicts structural deviations, not outcome deviations.

Three realistic experimental signatures (carefully framed):

  • Recursive-depth–dependent decoherence:
    τ-stability timescales depend on nesting depth, not just environment. This could appear as anomalous scaling in multi-layer measurement setups.
  • Context-sensitive entanglement decay:
    Same entangled system, different recursive measurement hierarchies → different stability profiles. Not a violation of QM, but structure-dependent decoherence.
  • Non-Markovian residual correlations:
    Instead of claiming "Φ-resonance," a grounded phrasing is: correlations that cannot be attributed to environment alone.

A crucial wording shift keeps this honest and testable:

UNNS predicts where standard assumptions about independence and locality break down structurally, not statistically.

3.1. Concrete Experimental Designs

Testability requires specificity. Here we outline three experimental protocols that could distinguish UNNS predictions from standard quantum mechanics:

Protocol 1: Nested Measurement Decoherence

Source Layer 1 d=1 Layer 2 d=2 Layer 3 d=3 Detector τ₁ τ₂ τ₃ UNNS: τ scales non-linearly with recursion depth d

Prediction: Standard QM expects decoherence time to depend only on environment coupling. UNNS predicts additional depth-dependent scaling: τ(d) ∝ f(d) · τ_env where f(d) is a non-trivial function of nesting depth.

Protocol 2: Context-Sensitive Entanglement

Prepare identical entangled pairs. Subject one set to hierarchical measurement contexts (nested interferometers), the other to flat measurement. UNNS predicts correlation decay rates will differ even with identical environmental coupling.

Protocol 3: Φ-Resonance Signatures

Look for correlated fluctuations in ostensibly independent quantum systems sharing similar generative histories (same preparation protocol, different spatial locations). These would manifest as non-Markovian correlations unexplained by environmental channels.

3.2. The Recursion Depth Parameter

One of UNNS's most distinctive features is the explicit treatment of recursion depth as a physical parameter. The Phi-Regime paper formalizes this:

d ∈ ℕ (recursion depth)

Gen_d : Φ → H(C)
R_{d→d+1} : H(C) → H(C)

Coherence condition:
Gen_{d+1}(φ) ≈ R_{d→d+1}(Gen_d(φ))

This structure implies that quantum states at different recursion depths are not merely differently labeled—they have genuinely different stability profiles.

Φ d=1 d=2 d=3 Ψ₁(d=1) Ψ₂(d=2) Ψ₃(d=3) Recursive Unfolding from Φ Each depth layer has distinct τ-stability properties

This is where UNNS diverges most sharply from standard interpretations. Copenhagen, Everett, and even QBism treat all measurement contexts as fundamentally equivalent. UNNS predicts they are not: structural depth matters physically.

4. How to Present This Cleanly

If this is presented as a follow-up article or talk, the structure matters. These section titles consistently communicate the substrate shift:

  • Why "Collapse" Was the Wrong Question
  • Observers Without Minds
  • Φ Is Not a State
  • Bell Violations Without Hidden Variables
  • What Would Falsify UNNS?

One sentence should anchor the entire presentation:

UNNS does not modify quantum mechanics; it modifies what we think quantum mechanics is about.

4.1. Bell Violations Without Hidden Variables

A frequent misunderstanding is that any substrate-level theory must be a hidden variable theory. The Phi-Regime paper addresses this directly: Φ does not assign definite pre-measurement values.

Instead, Bell violations emerge naturally from shared generative structure:

Corr(A, B) ~ shared_generative_origin

Not: λ hidden variables
Not: FTL signaling
But: Common Φ ancestry
Shared Φ-origin Observer A τ-filter Observer B τ-filter Correlated via shared ancestry, not signaling ✗ No causal link

This resolves the apparent paradox: correlations stronger than local realism allows, yet no mechanism for signal transmission. The correlations are structural, not causal.

4.2. What Would Falsify UNNS?

A theory that cannot be falsified is not physics. UNNS makes specific claims that could be experimentally refuted:

  • Falsification 1: If decoherence times show no dependence whatsoever on measurement hierarchy depth (holding environment constant), the recursion-depth prediction fails.
  • Falsification 2: If entangled systems with identical preparation histories show no correlation signatures beyond standard environmental coupling, the Φ-resonance hypothesis is wrong.
  • Falsification 3: If nested interferometry experiments show perfect Markovian behavior with no context-dependent anomalies, the Ψ-projection structure collapses to standard QM.

Critically, these are not "interpretation differences"—they are empirical predictions about measurable timescales, correlation patterns, and stability profiles.

UNNS stands or falls on structure, not statistics.
Standard QM predictions UNNS extensions Shared Depth scaling Φ-correlations Non-Markovian Falsifiable predictions in the extended region

4.3. The Role of Operator XII

The Axiomatic Hierarchy paper mentions Operator XII among the inter-regime operators. While the full formalism is reserved for technical work, its conceptual role deserves clarification:

Operator XII: Elimination of non-survivable structure

This is not collapse in the Copenhagen sense. It is the structural pruning of Ψ-flows that fail to meet τ-stability thresholds. The operator acts as a retroactive consistency filter rather than a forward-time reduction.

Multiple Ψ-flows Op-XII τ-pruning Stable outcome Pruned Pruned S(Ψ) ≥ θ Selection without ontological reduction

This mechanism preserves the no-collapse unitary evolution at the Φ-Ψ level while still producing definite outcomes at the τ level. It's a many-to-one structural filter, not a many-worlds branching.

5. Bottom Line

This program is not hand-wavy. It is structurally realist, ontologically disciplined, cautious about predictions, aligned with modern decoherence theory, and genuinely novel in how it separates generability from probability.

Most importantly, the claim is not "QM is wrong." The claim is:

Quantum mechanics starts too late in the story.

UNNS supplies the missing earlier chapters: generability (Φ), relational projection (Ψ), and stabilization (τ) — treated as substrate-level regimes rather than observer-dependent mysteries.

Φ Generability Ψ Projection τ Stability

6. Broader Implications for Physics

If the UNNS substrate picture is correct, several established frameworks require careful re-examination:

Quantum Field Theory

QFT treats fields as fundamental. In UNNS, fields are Ψ-regime structures—highly successful approximations to deeper Φ-generability. The Φ-substrate suggests QFT should exhibit subtle departures in extreme recursion scenarios (nested vacuum states, hierarchical measurement contexts).

General Relativity

Spacetime is typically treated as the stage on which physics unfolds. UNNS inverts this: spacetime structure emerges from τ-stabilization of geometric Ψ-flows. This opens paths toward reconciling QM and GR through substrate-level unification.

Information Theory

Shannon information assumes pre-existing symbols. UNNS adds a prior layer: how do information-bearing structures become possible? The Φ-regime provides generative capacity; τ-stability provides preservation. Information emerges at the interface.

The substrate is not an addition to physics—it is a recognition of what was always implicitly assumed but never formalized.

7. Philosophical Context and Precedents

While UNNS is novel in its specific formalization, it draws on deep philosophical traditions:

  • Structural Realism (Ladyman, Ross): UNNS accepts that structures, not objects, are fundamental—but adds recursive dynamics.
  • Process Philosophy (Whitehead, Bergson): Reality as becoming rather than being aligns with Φ-generability preceding Ψ-actualization.
  • Modal Realism (Lewis): UNNS treats possible states seriously but grounds them in generative structure rather than disconnected worlds.
  • Dispositional Ontology (Mumford, Anjum): Φ represents dispositional structure—potentials constrained by generative rules.

What distinguishes UNNS is mathematical rigor combined with empirical testability. It is not metaphysical speculation—it is structural ontology with experimental consequences.

References

Throughout this article, UNNS is treated as a substrate ontology: it explains why quantum mechanics works where it does, not how to replace it.

UNNS Substrate — Unbounded Nested Number Sequences / Universal Network Nexus System
A recursive substrate approach to foundational mathematics and physics
© 2024-2025 UNNS Research | unns.tech

Main Menu