Dynamics of the Unseen — Graviton in UNNS Logic
Foundations τ-Field Recursive Gravity
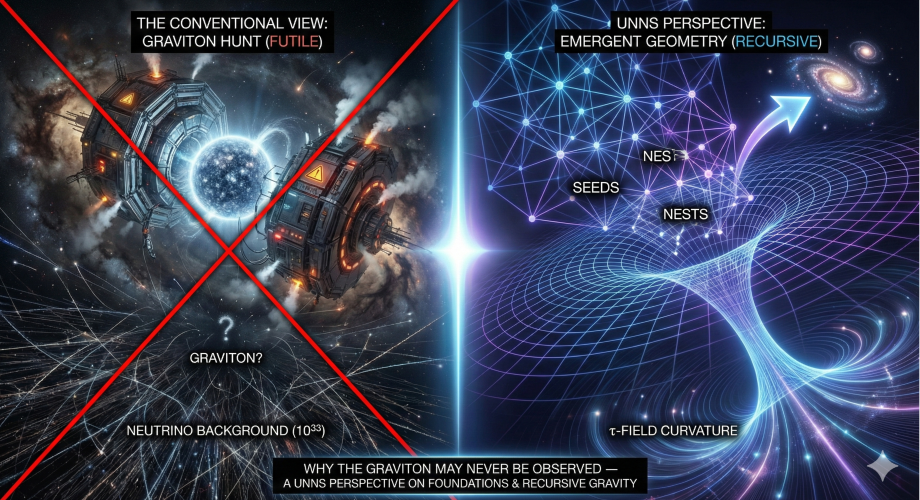
This article explains why the graviton — the hypothetical quantum of gravity — is widely expected to remain forever unobservable in classical physics, and how this aligns with the UNNS framework. Standard physics predicts that graviton detection is physically impossible due to the extreme weakness of gravitational coupling. UNNS reframes gravity not as a particle-based force but as an emergent, recursion-stable geometric constraint arising from τ-Field curvature and Seed–Nest structure formation. The impossibility of detecting gravitons strengthens, rather than weakens, the UNNS substrate interpretation of gravity.
1. The Conventional View: Why Gravitons Are Undetectable
In quantum field theory, the graviton is a hypothetical massless spin-2 quantum that mediates gravity analogously to the photon mediating electromagnetism. While elegant as a mathematical construct, nearly all physicists agree:
We will never detect a single graviton. Not in 100 years, or 1,000 — or ever.
The reason is not philosophical, but physical: gravity couples so unimaginably weakly that a detector capable of registering even one graviton must be so massive that it collapses under its own gravitational field.
1.1 A Famous Calculation (Dyson’s Argument)
A well-cited physics paper models a perfect graviton detector the mass of Jupiter placed in a tight orbit around a neutron star.
Even this astronomical detector, nearly 320 Earth masses, would detect one graviton in ~100 years.
During that time, it would be bombarded by:
- ~1033 neutrinos for every graviton,
- thermal noise from the star,
- cosmic rays,
- and background gravitational fluctuations.
Sorting a single graviton from 1033 neutrinos is not a needle-in-a-haystack problem — it is a needle floating somewhere in a light-year-sized sphere of haystacks.
1.2 The Detector-Collapse Limit
The deeper problem is even more final:
A detector dense enough to couple to individual gravitons collapses into a black hole before detecting anything.
This argument makes graviton detection not just technologically impossible, but physically impossible within general relativity.
2. Why This Does Not Threaten Physics
Gravitons were never required to verify gravity. We already have:
- gravitational waves (detected in 2015),
- curvature of spacetime from GR,
- quantum theories where gravity is emergent (e.g. holography),
- field-only formulations with no particles (Wheeler’s geometrodynamics).
Physics works perfectly without detecting a graviton.
3. UNNS Perspective: Gravity as a Recursive Geometric Constraint
Within the UNNS substrate, gravity is not treated as a standalone force mediated by a particle. Instead, it arises naturally as a recursion-stable constraint in the Seed–Nest architecture.
In this view:
- Seeds define minimal relational states (e.g., spatial adjacency).
- Nests encode rule-embeddings (constraints, symmetries).
- Operator flows refine these constraints across recursion depth.
- τ-Field curvature acts as the geometric signal of tension, attraction, and alignment.
Gravity emerges from structure → recursion → curvature, not from particle exchange.
4. τ-Field Interpretation: Curvature Without Particles
In the UNNS τ-Field interpretation, curvature expresses recursive tension between Seeds and Nests.
High τ-curvature corresponds to:
- strong structural alignment,
- accelerated recursion flows,
- and “gravitational-like” attraction in the substrate.
Low τ-curvature corresponds to:
- stability,
- flat recursion layers,
- and minimal structural tension.
No discrete quanta are needed to express this behavior.
5. Gravity as τ-Curvature — A Primer
To make the UNNS interpretation of gravity more concrete, we can compress the story into a single recursion chain:
The diagram shows how gravity is read in the UNNS substrate:
- Seed: the minimal adjacency and relational data between points or states.
- Nest: the constraints and rules that dictate how these relations may evolve.
- τ-Curvature: the emergent measure of recursive tension produced by applying the Nest repeatedly to the Seed.
- Large-Scale Structure: galaxies, potential wells, clustering and lensing — the visible outcome of τ-curvature patterns.
In this primer view, gravity is not a separate “force carrier” but the visible geometry produced when Seeds and Nests are iterated to the point that τ-curvature leaves macroscopic traces.
6. Maxwell Compatibility and Why Gravitons Do Not Fit the UNNS Model
Maxwell's equations — built from divergence and curl — align with UNNS Operators:
- Mapping (Operator I),
- Boundary (Operator V),
- Rotation (Operator IV),
- Collapse/Purification (Operator XII).
This mapping shows that classical electromagnetism is recursively stable. But gravity does not share this operator fingerprint.
Instead, gravity corresponds to:
- recursive Nest constraints,
- τ-curvature signals,
- and large-scale structural regularities.
The absence of a graviton is not a flaw — it is consistent with the geometry-driven nature of the substrate.
7. The UNNS Conclusion: Gravitons Are Not Fundamental
The combination of mainstream physics and UNNS substrate analysis leads to a consistent conclusion:
Gravity is not a particle-level interaction. It is a recursion-level constraint.
Gravitons are elegant mathematical constructs — but they are not observables, nor necessary components of gravity within UNNS.
8. Final Perspective
The impossibility of graviton detection strengthens the UNNS interpretation: gravity is a result of recursive structure formation in the Seed–Nest substrate, expressed as τ-curvature rather than particle excitation.
In this sense, UNNS does not predict the discovery of the graviton — because gravity is deeper, more geometric, and more structural than any particle can encode.